电场

高斯定理

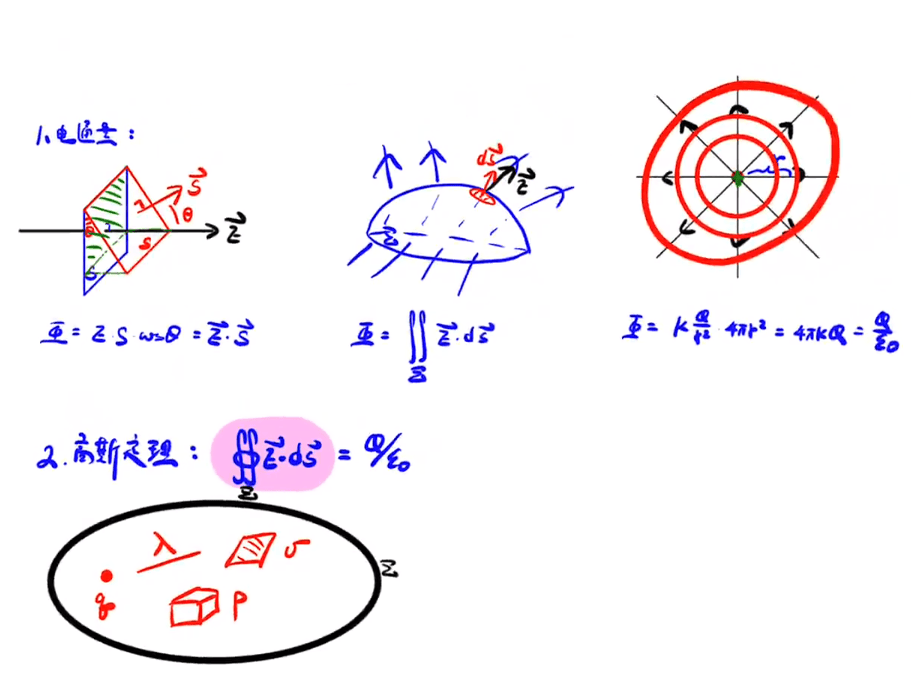
1. 电通量

   传过某个面的电场线的条数

   电场代表了电场线的疏密，电场×面积就能代表电场线的条数，即电通量，可类比磁通量用$\Phi $来表示

2. 证明过程（不严谨）

3. 高斯定理表达形式

   $\oiint E dS=\dfrac{Q}{\varepsilon _{0}}$​ （注意对面积进行积分而不是体积）​

   其中$\varepsilon _{0}$满足$\varepsilon _{0}=\dfrac{1}{4\pi k}$

4. 高斯定理的应用

   

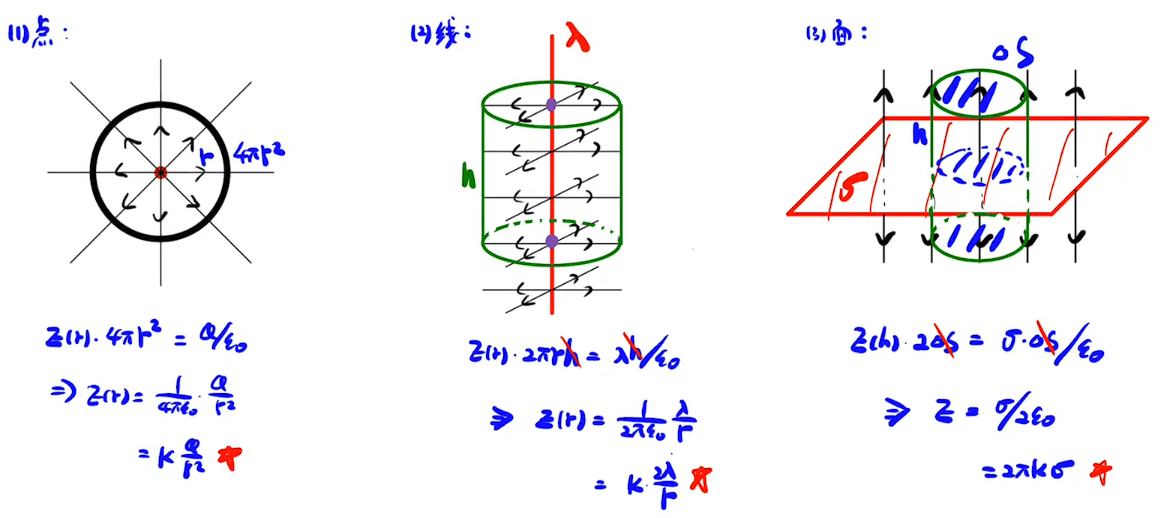
注意：

高斯面的对称是为了保证处处电场相等，你如果选取的高斯面球心不在中心，那E就是个变量，是所有不同E的平均值，

虽然算出来的结果和正确答案一致，但没有实际意义，充其量算一个没啥用的等效电场

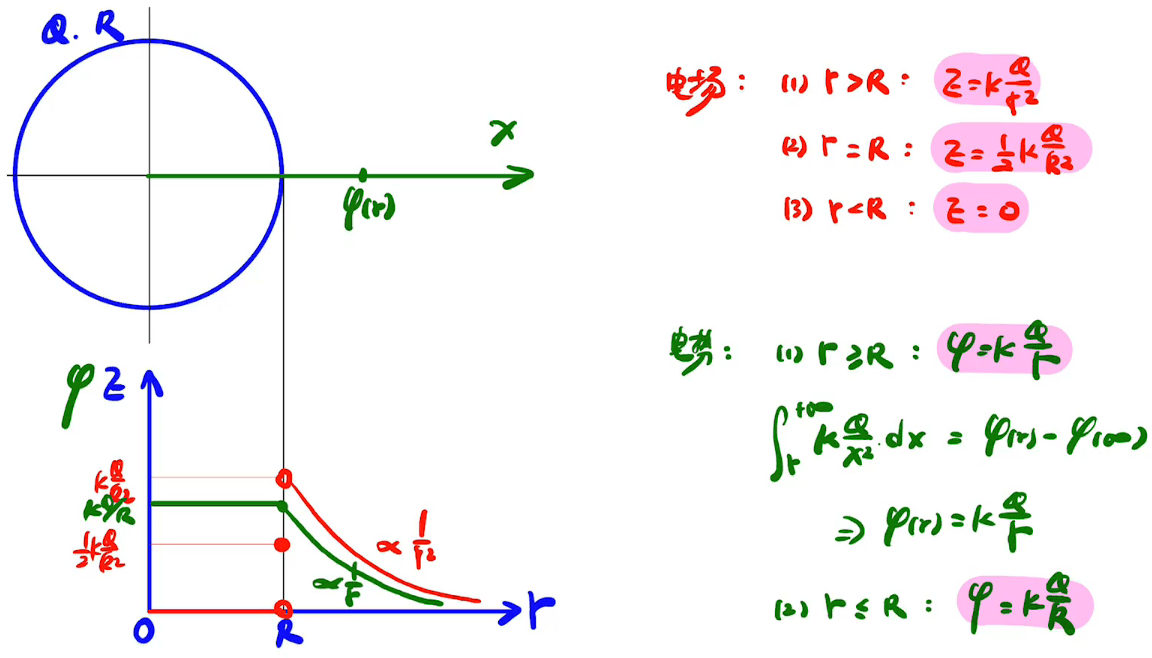
电场 电势能 电势

电势与电场之间的关系是导数与原函数的关系（对路径进行求导或积分）

$-\nabla \varphi =\overrightarrow{E}$​

$\varphi =-\int Edx$​

安培环路定理

$\oint Edl$​​​ 即电势差，在闭合回路中电势差为0.

自势能

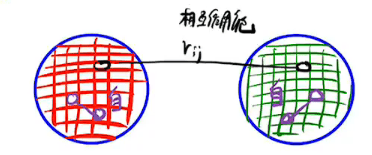
两个球之间的电势能在计算时要减一半

例如两个相同电荷Q之间的电势能就是$\dfrac{kQ^{2}}{2r}$​ ​

一个系统的电势为下图，也可以写成$\dfrac{1}{2}\sum \dfrac{kQ_{i}Q_{j}}{r_{i\rightarrow j}}$，其中$\dfrac{kQ_{j}}{r_{i\rightarrow j}}=\varphi$

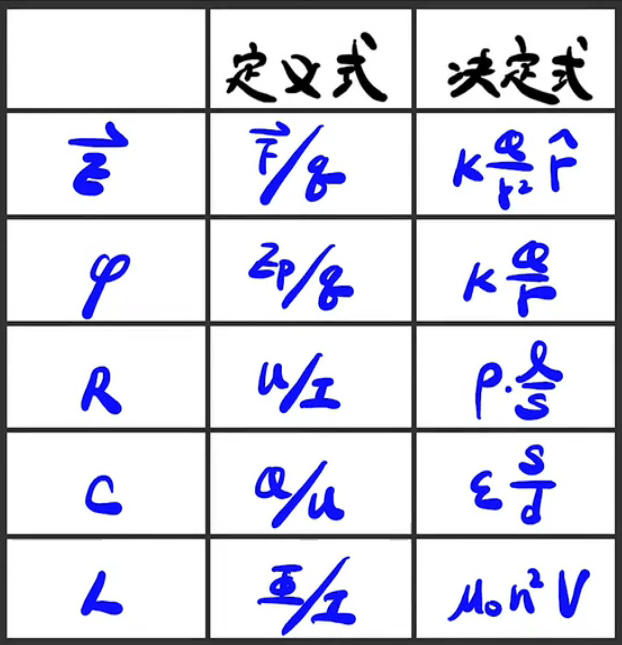
各种概念总结

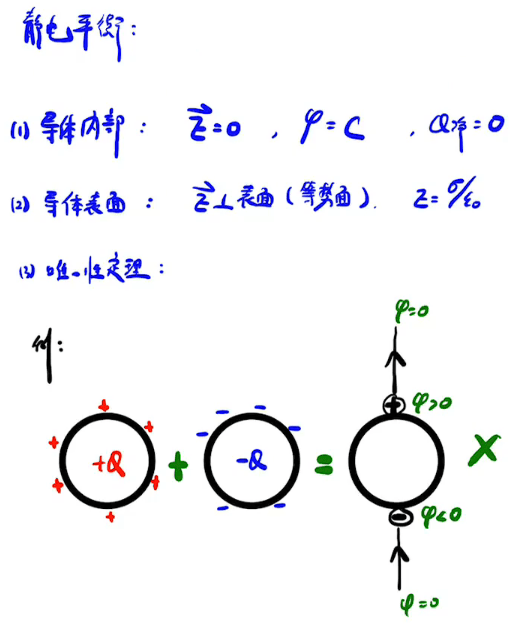
静电平衡的条件

• 题目

题目感悟：

1. 若存在多个同心圆式球壳，内部的电荷不会影响外部的电势
2. 充分利用导体内部电势为0的条件
3. 接地之后外部电势即为0

电像法

前提：静电平衡的唯一性定理

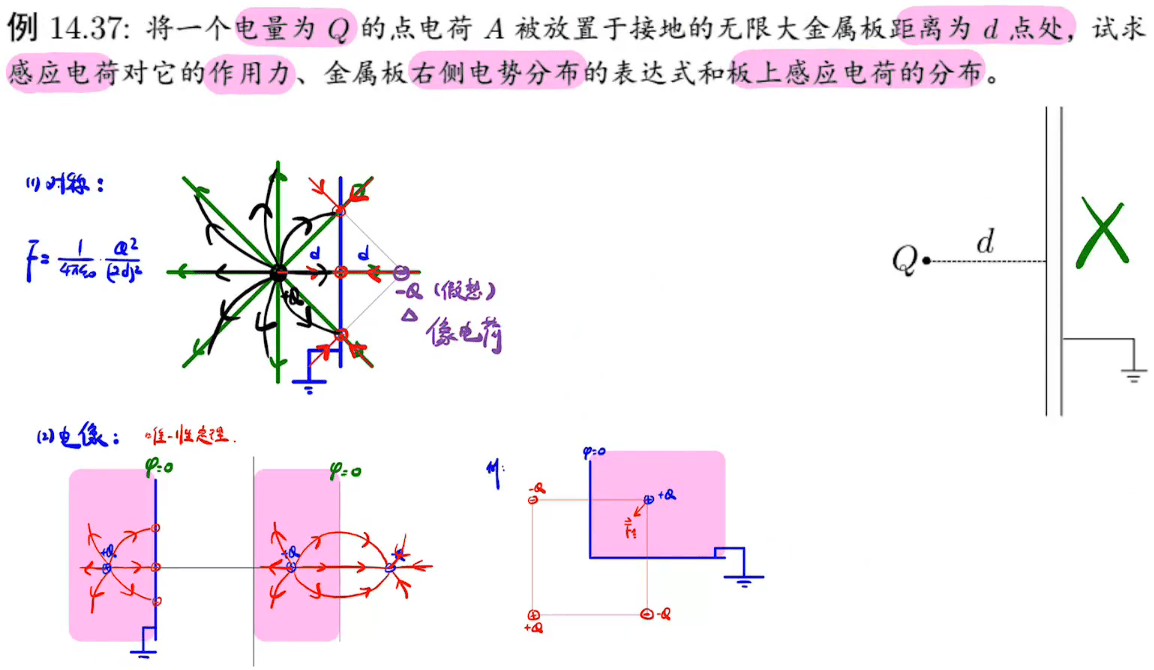
在镜像法中，外力做的功是自势能的一半

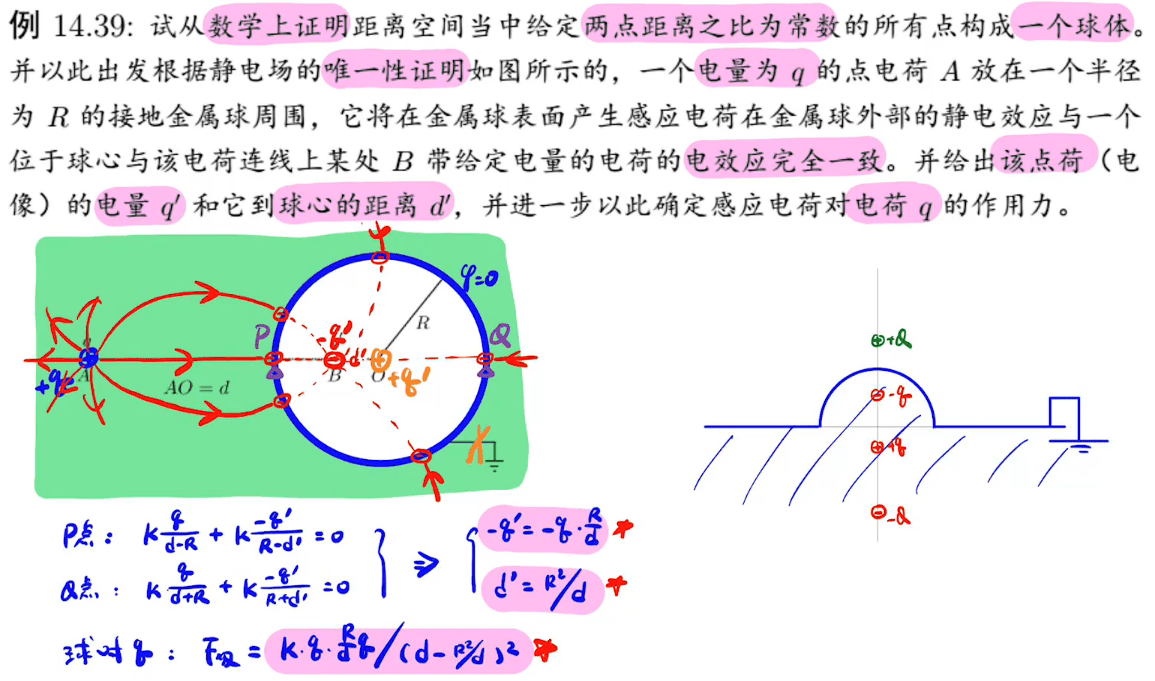
电像法还要保证最终合成电势为0，不能凭空加一个负电荷就完成了

如果不接地的话，在中间加上一个正电荷形成等势面。

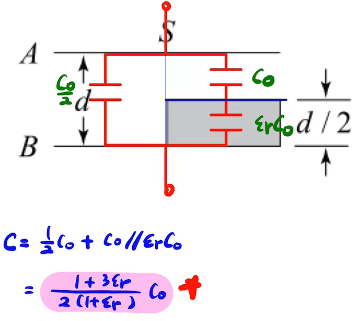
电容

基础概念

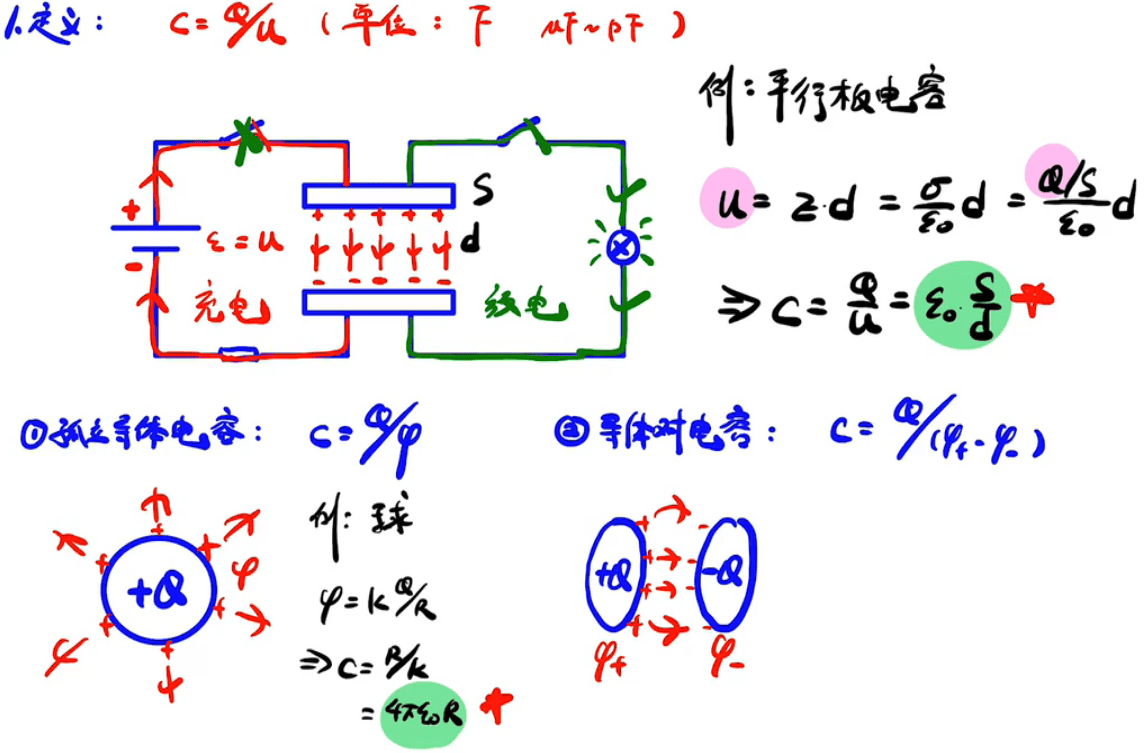
隐含条件

• 题目：

  

  

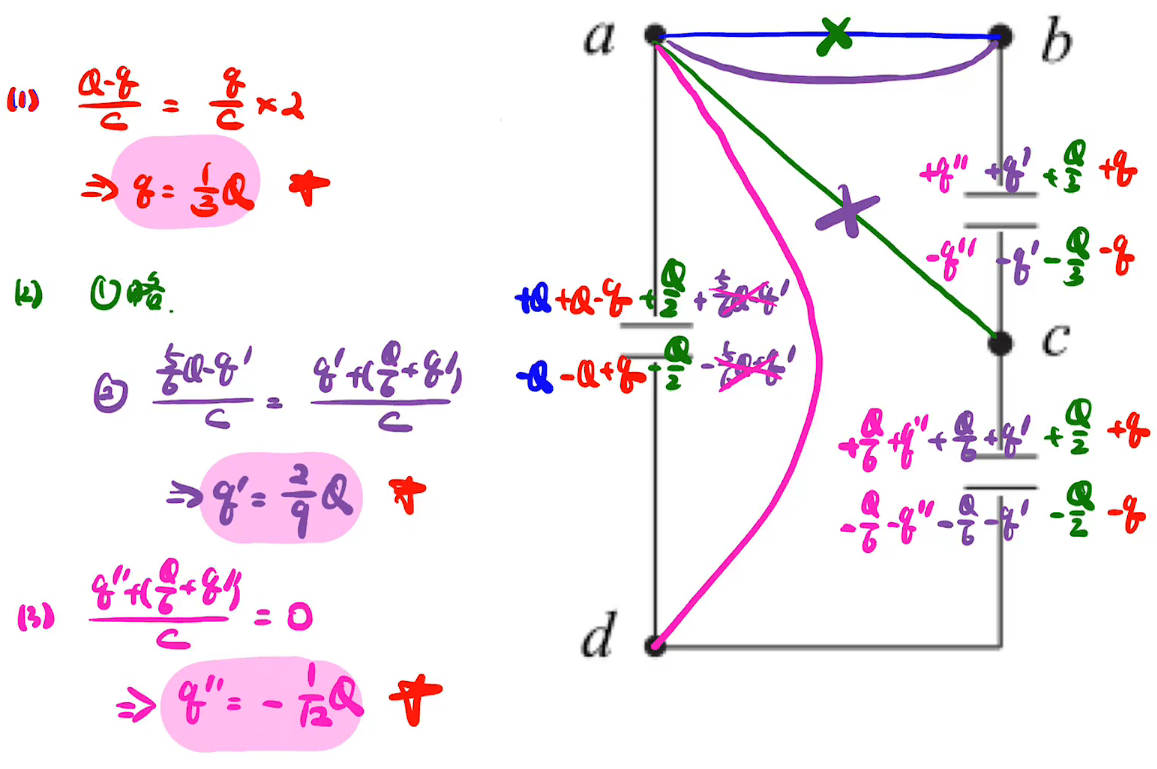
  抓住转一圈电压相等和孤岛效应进行求解

  并且有稳定时刻左右电压相等

  能量问题

  

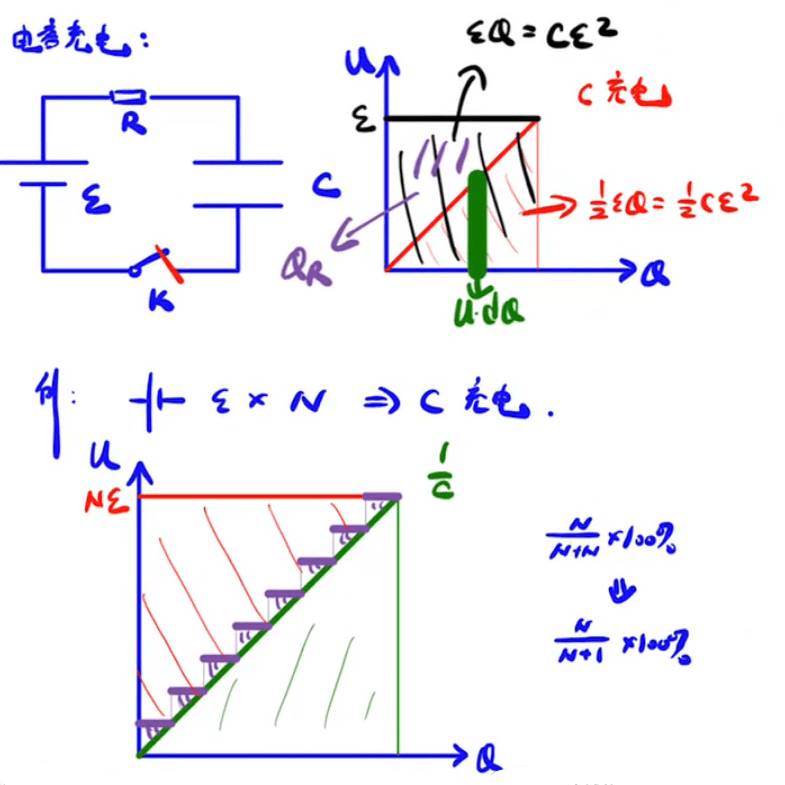
  等效法

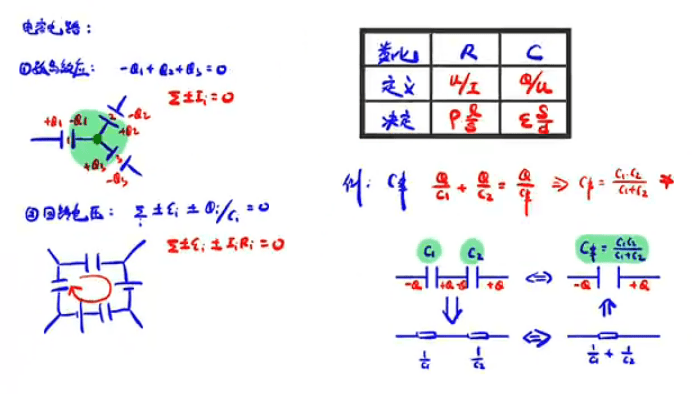
  1. 将电容的倒数作为电阻，求出总电阻之后取倒数即可得到总电容

     例题（与上面不同）

     

  2. 直接读出电容串并联

     • 

恒定电流

电流面密度 J

• 定义：

  • $I=\sum _{s}j\Delta S\cos \theta =\int _{s}\overrightarrow{j}d\overrightarrow{S}$​​

    其中 I 为电流强度，j 为电流密度（即单位体积的电量）

  • $\overrightarrow{j}=\rho \overline{v}=nev$ ，$\rho$为电阻，n为电流体密度

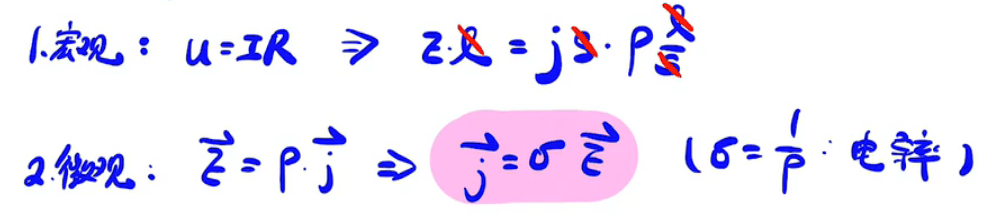
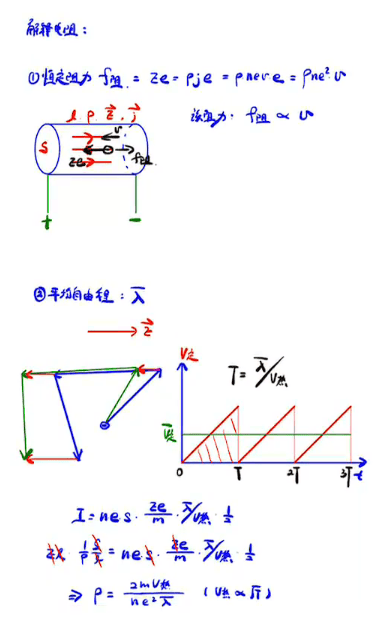
电阻的两种解释

Y与△型电路变换

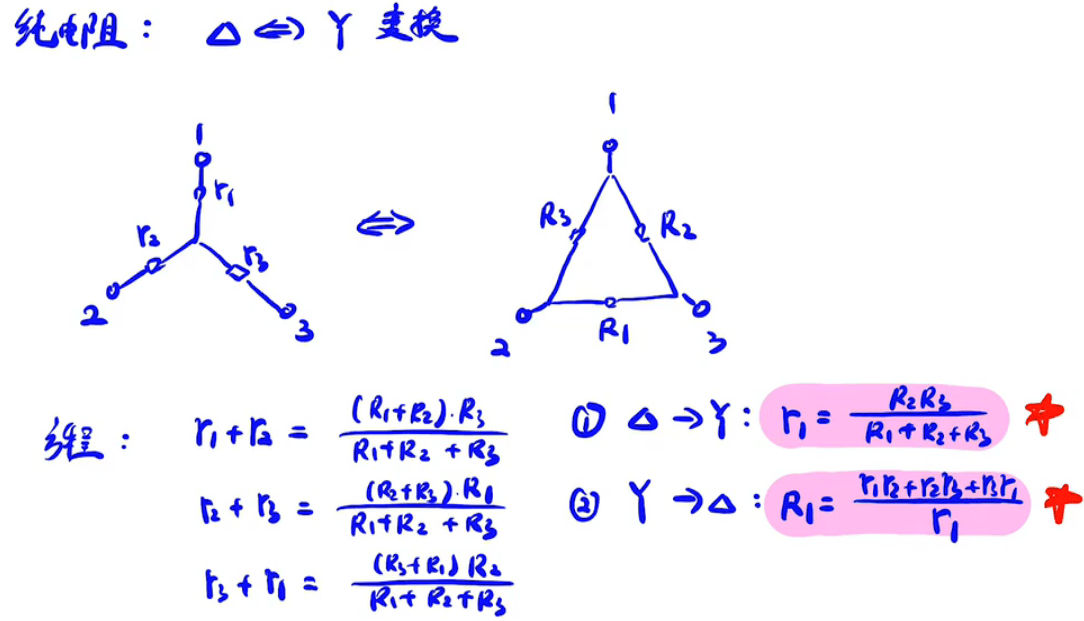
例如：

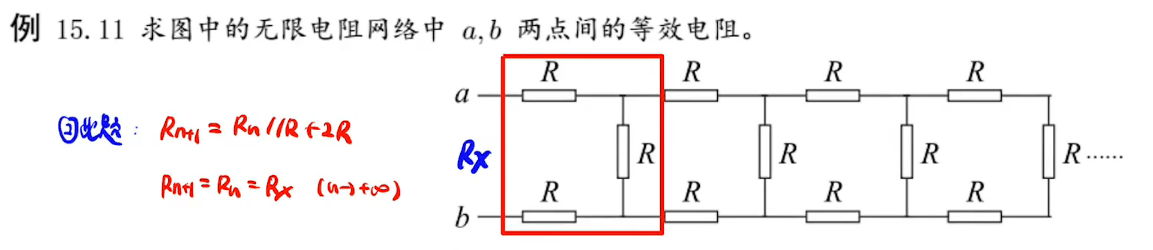
无限电阻

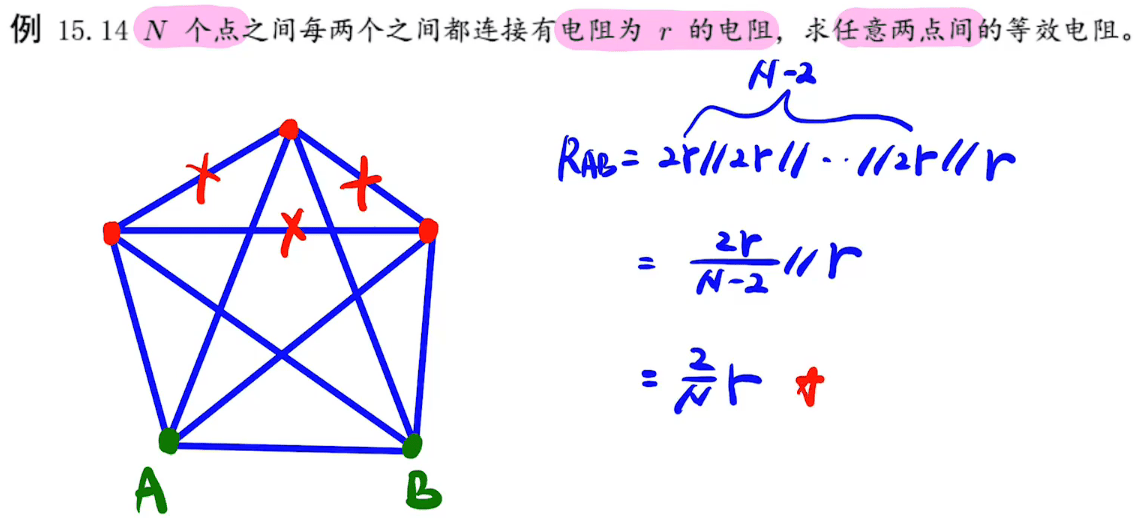
1. 自相似及自全等类

   

   

2. 等势点可短可断

   

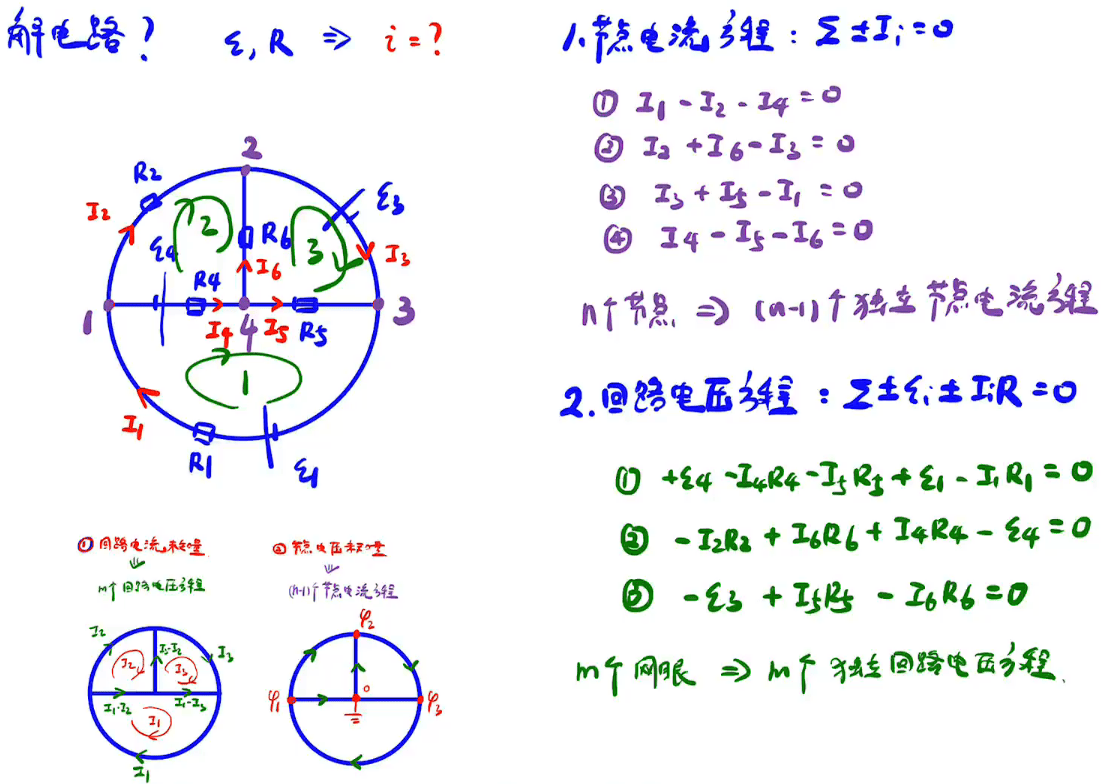
基尔霍夫定律

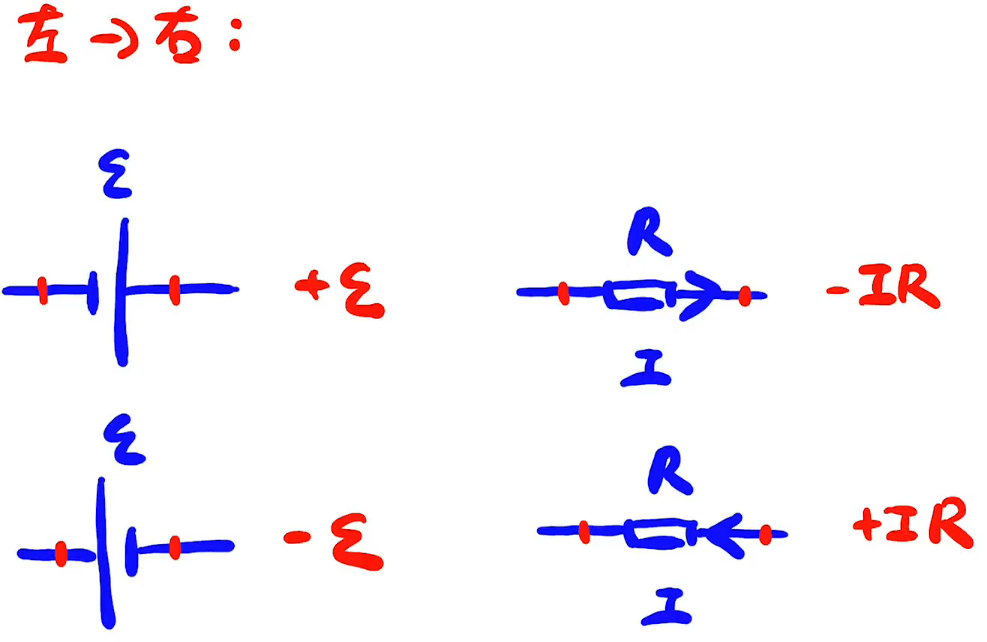
等效电压/流源

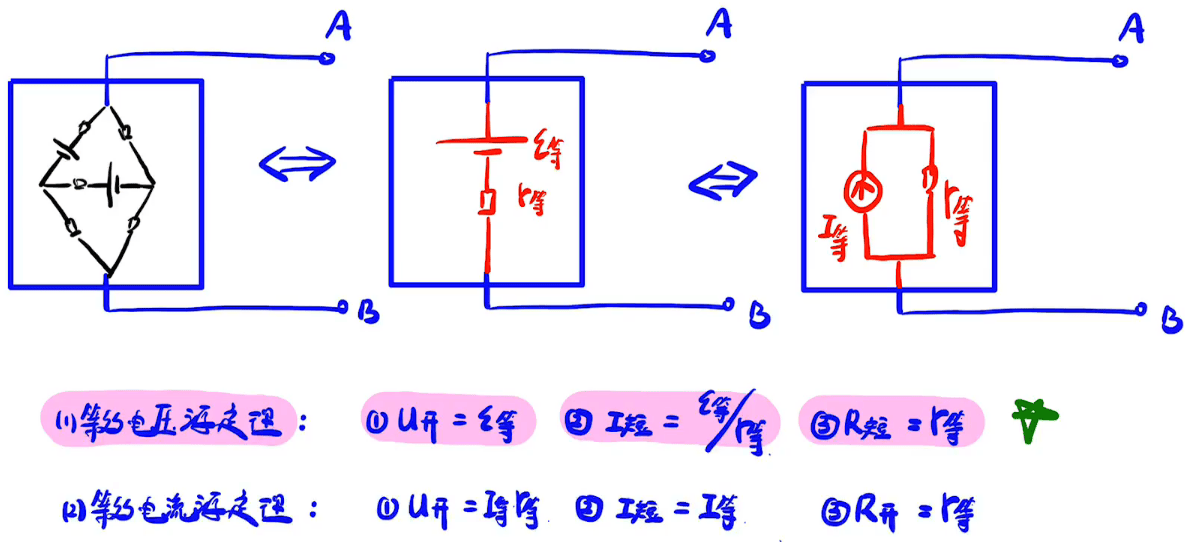
• 应用

  

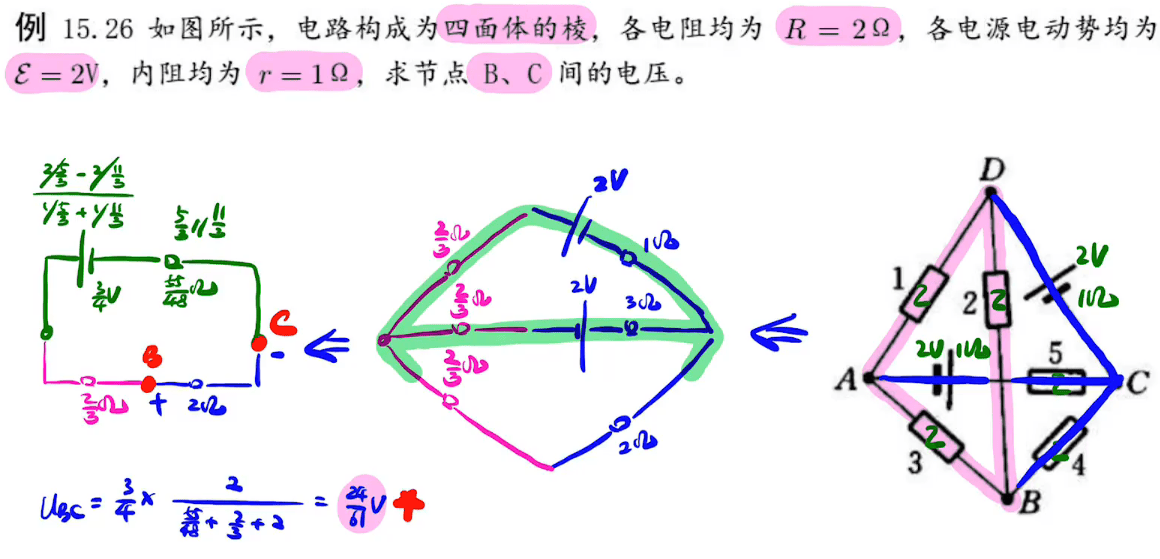
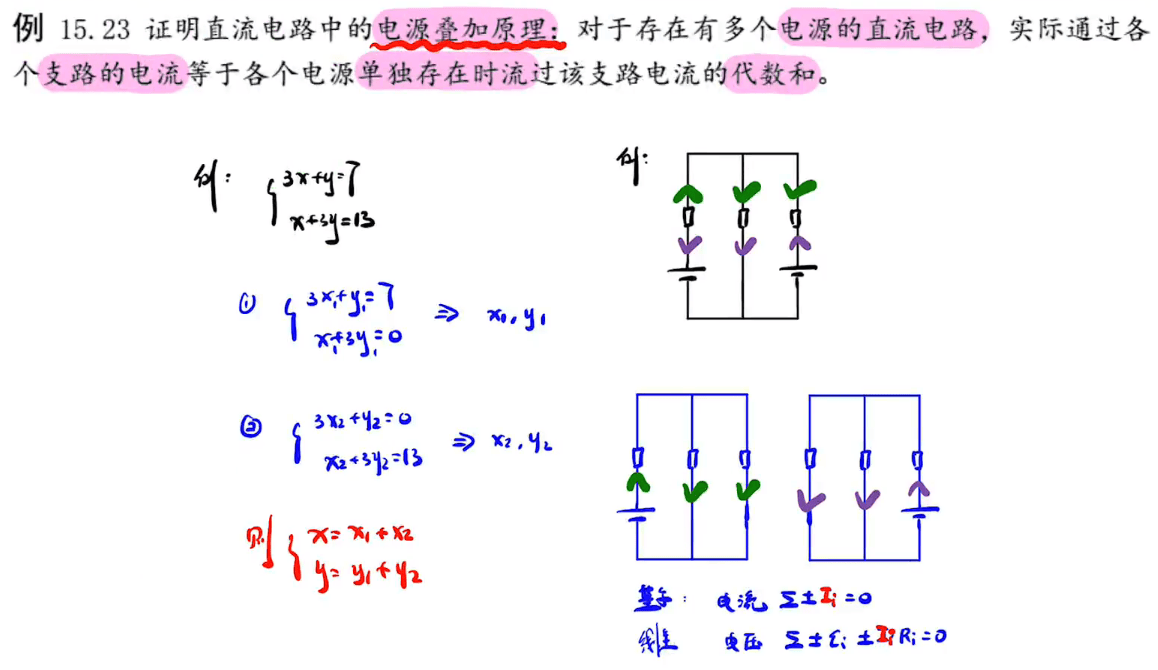
电源叠加原理