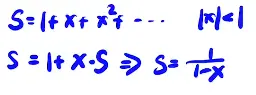菜菜

运动学

第一课时

1. 关于质心

过重心的线
面积不一定等分

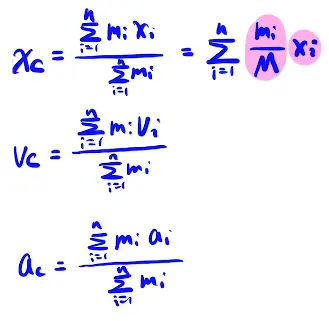
2. 一维运动

（物理常在对应物理量上加点来表示对时间的导数)

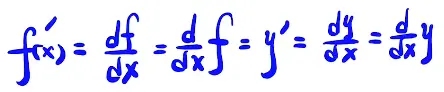
求导公式。上两个为导数公式的不同形式，如果是两个点就表示二阶求导，如图

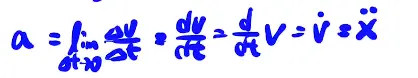
速度即为路程的导数

第二课时

1. 坐标系

先拿张图镇楼

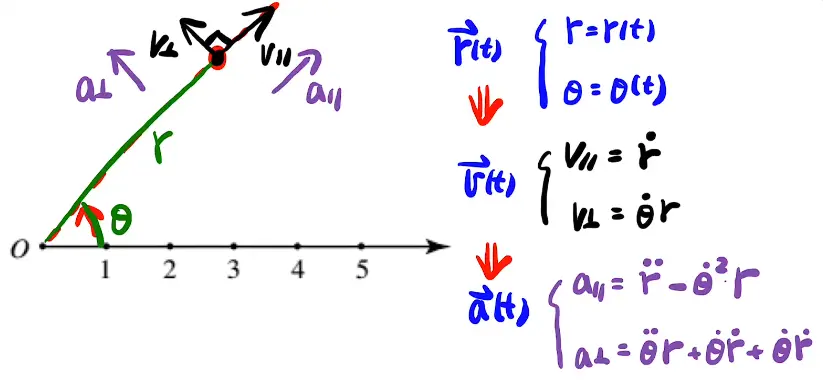
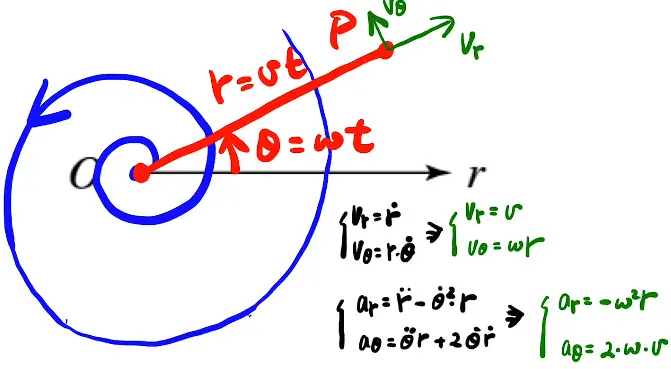
极坐标系中，位氏可以用r与$\theta$​​的参数方程来表示，即$\overrightarrow{r}=\begin{cases}r\left( t\right) \ \theta \left(
t\right) \end{cases}$​​​​这种形式。

对它求导即可得到速度，用自然坐标系（即将其分解成径向与切向）来表示。例如。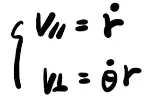

一道关于极坐标系的题目（注意自然坐标系的应用）

2. 速度

• 注意运用速度是路程的增长率，速度转移到路程来解
• 没啥好说的，分辨一下dr的各种形式吧

3.圆周运动

• 加油站⛽

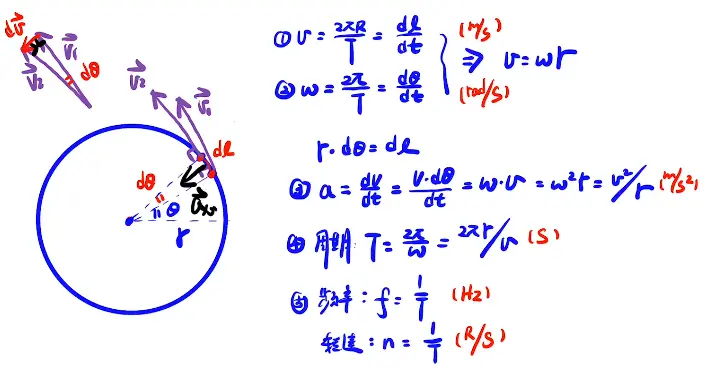
微元法理解：r沿着圆心有了速度ωr,速度沿着圆心做圆周运动就有了加速度$\omega ^{2}r$​

• 注意相对角速度的运用。

• 如果多个围绕共同圆心作匀速圆周运动质点的周期T的平方与它们各自的轨道半径R的三次方成正比

  证明：

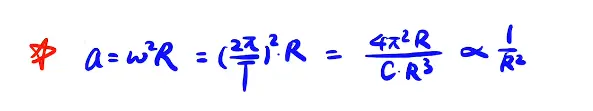
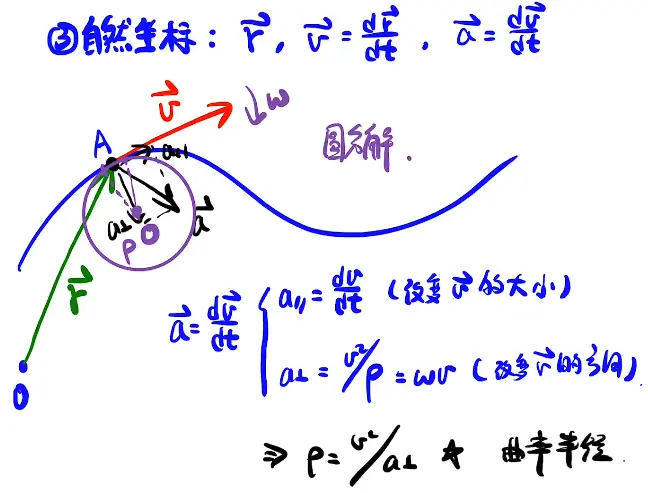
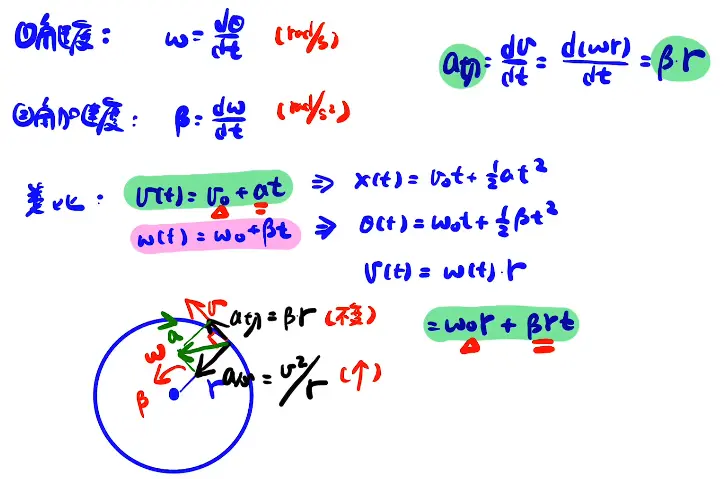
• 角加速度β

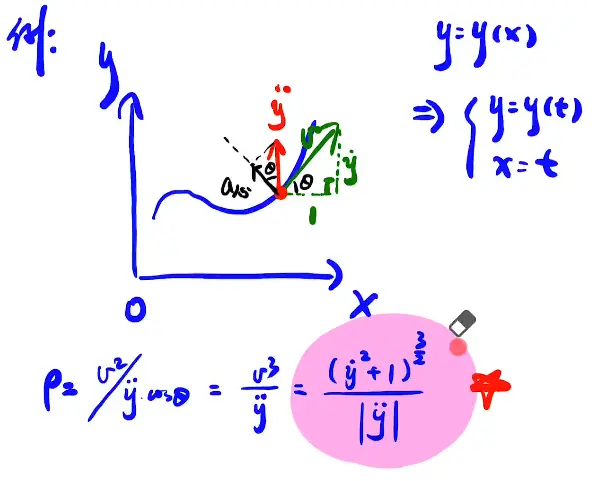
• 曲率圆及物理中数学的应用
• 
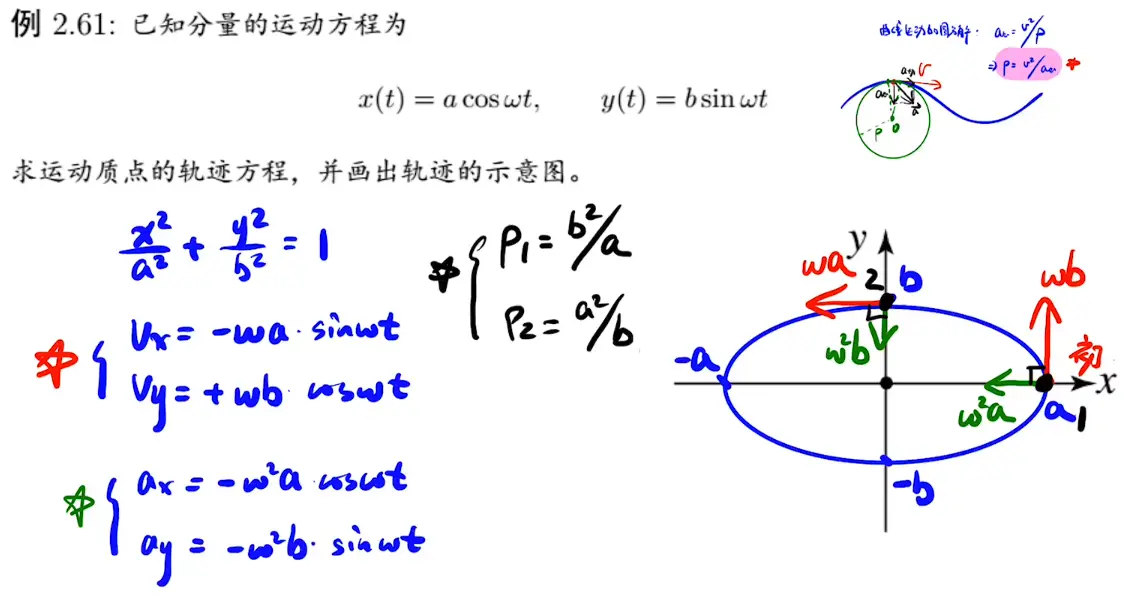
• 有关纯滚动（不打滑）

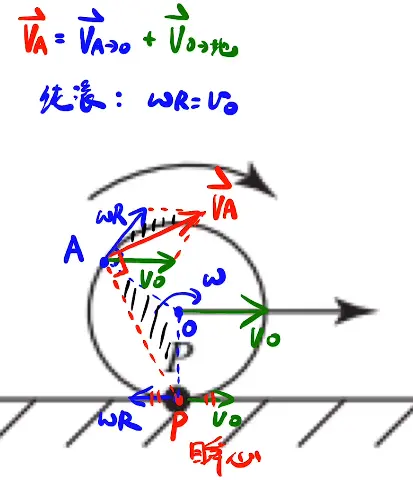
三角形AOP与速度三角形相似，由此可以推出

1. $\omega r=v_{0}$ ​
2. 某点合成速度与瞬心P的连线垂直

第三课时

1.相对运动

• 相对运动公式

  1.理解：

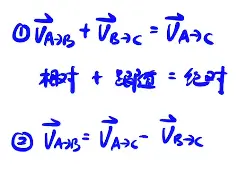
公式：$\overrightarrow{v}_{B\rightarrow A}$​=$\overrightarrow{v}_{B}$​-$\overrightarrow{v}_{A}$​

应用：

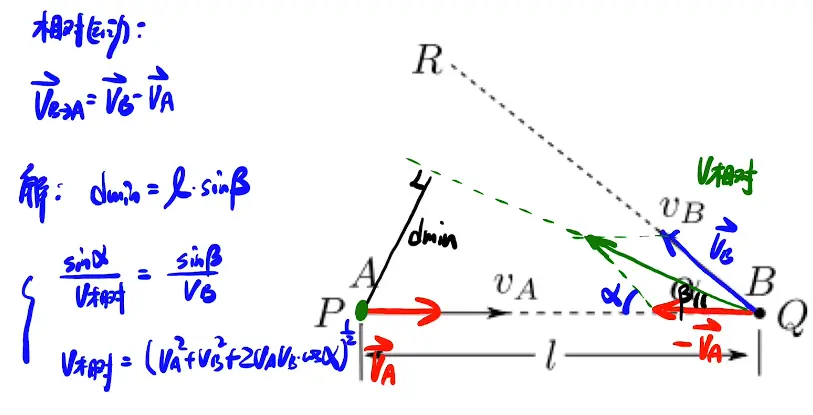
2.约束条件

• 有关杆，绳，点与面

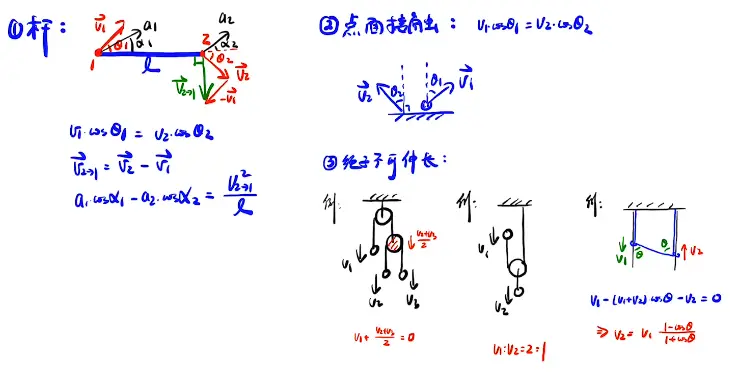
滑轮：上面定滑轮，下面的是动滑轮

• 模型构建

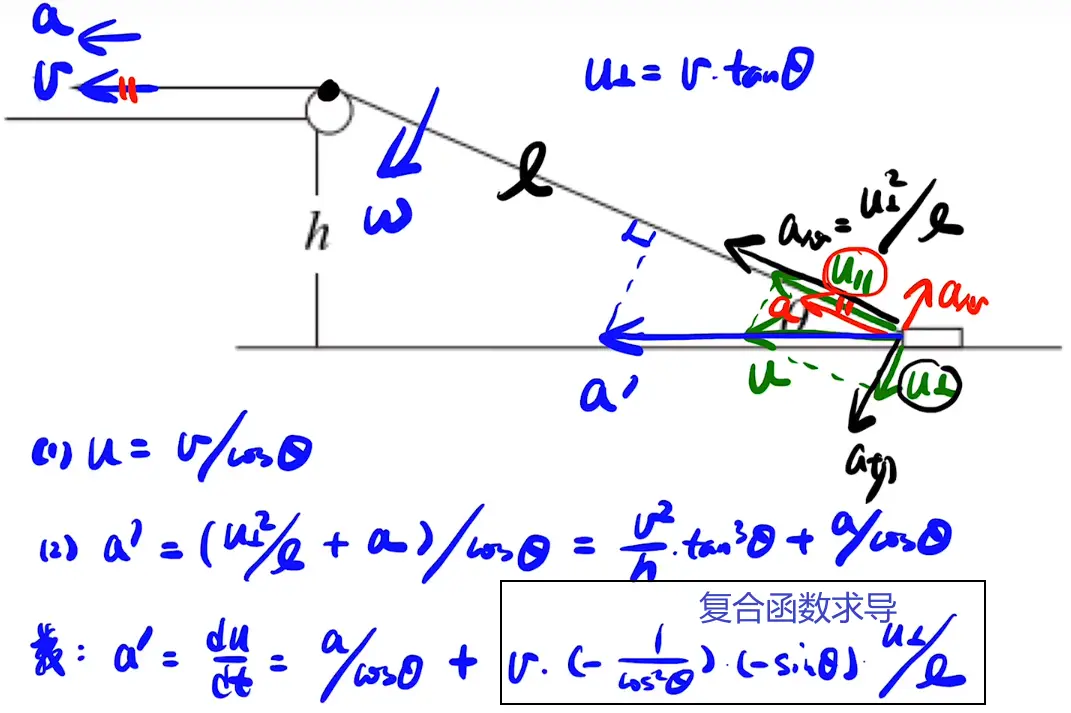
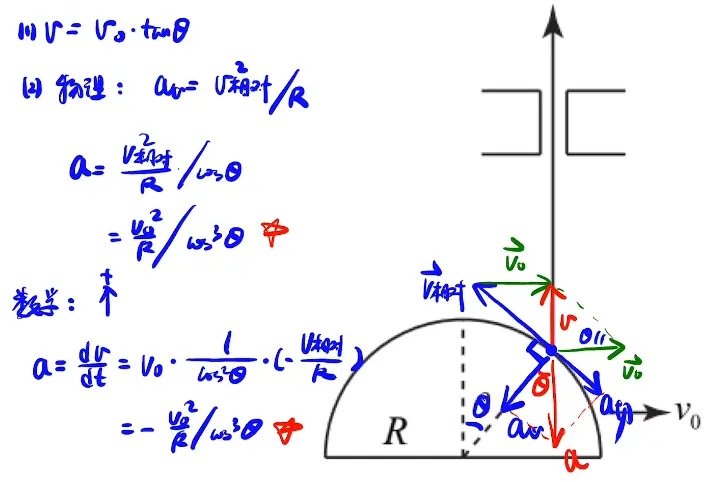
第四课时

1. 刚体运动

• 瞬心：在刚体运动的任意时刻都可以看成是围绕--个不动中心（相对地面）以给定的瞬时角速度转动，这个不动的中心称为刚体的瞬心，它可以在刚体内部，也可以在刚体外部。

2. 流体运动

• 

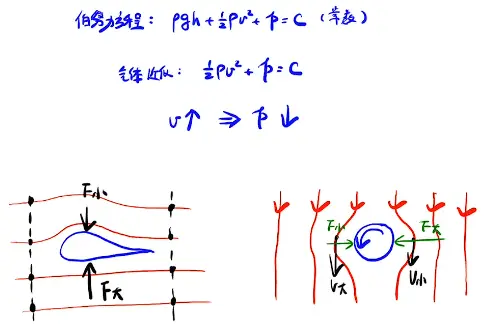
• 分类（以下图为例）：

  

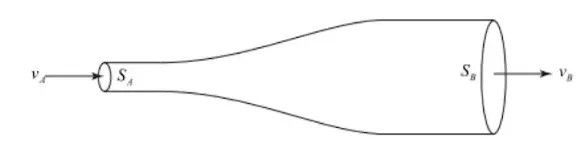
  1. 不可压缩（单位时间流入某截面的流量恒定）:$S_{A}v_{A}=S_{B}v_{B}=C$​​
  2. 稳定流动（单位时间流入截面质量恒定）：ρSv=C

数学奇技淫巧

数学基础
自相似

数学基础
利用物理方法求曲率圆的曲半径（生草)

数学基础：线性插值

离得十分接近可看做直线，29°到30°射程比3:2，角度也为3:2。