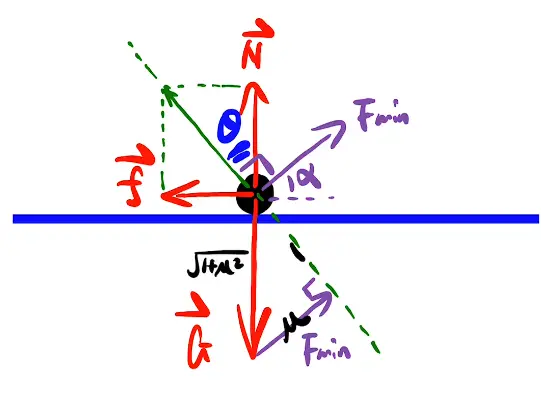
静力学
第一课时
1. 对称
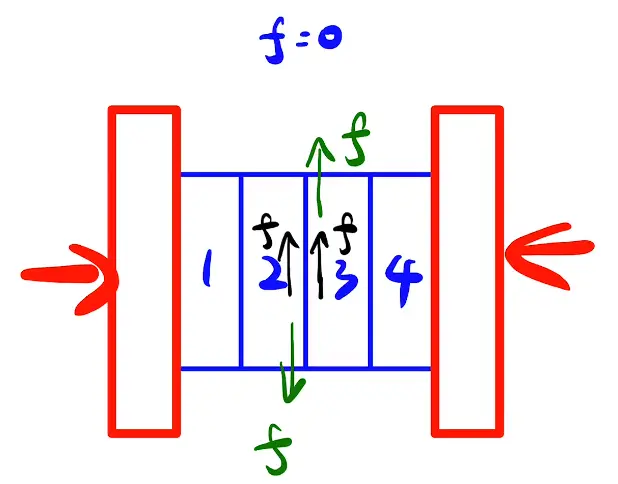
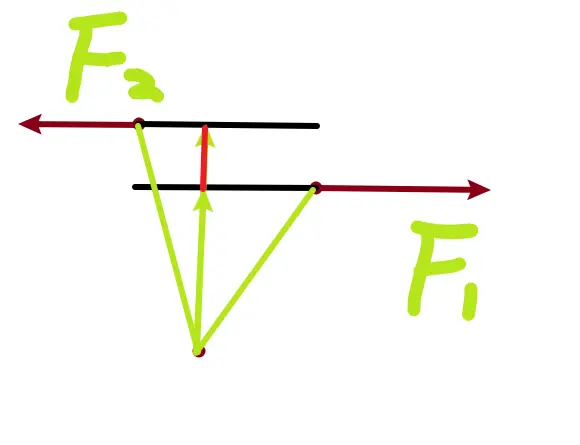
由以下两个条件可得f=0
- 对称的物理情境要有对称的物理受力分析,所以有了两个f,对称的因产生对称的果
- 相反作用力方向相反
2. 重心
- 定义:重心是指地球对物体中每一微小部分引力的合力作用点 [1] 。物体的每一微小部分都受地心引力作用(见万有引力),这些引力可近似地看成为相交于地心的汇交力系。由于物体的尺寸远小于地球半径,所以可近似地把作用在一般物体上的引力视为平行力系,物体的总重量就是这些引力的合力 [2] 。
- 注意重心必须依赖重力而存在。实际上,重心反映了重力“三要素”中的“作用点”要素,因此, 可以说重心是重力概念的一个派生概念。根据重心的定义,严格地讲,在地面上方的物体有重心的充分必要条件是作用在它各部分的重力的作用线是相互平行的。在地面上方的大物体不存在以上意义的重心[1]。可见,重心概念只对地球附近处受到地球引力的一切小物体有意义。
- 辨析:重心与物体所受的重力相联系,它实际上是重力组成的平行力系的中心,而质心与物体的质量分布相联系,它可视为一个特殊的“质点”,这个“质点”的质量同整个物体的质量相等,质心实际上是组成物体各质元的矢径的加权平均中心,所取的权重就是该质元的质量。显然,物体的质心只与物体各部分质量分布有关,而与重力无关。所以,质心概念对处于任何位置的任何物体都具有意义。
3. 弹力
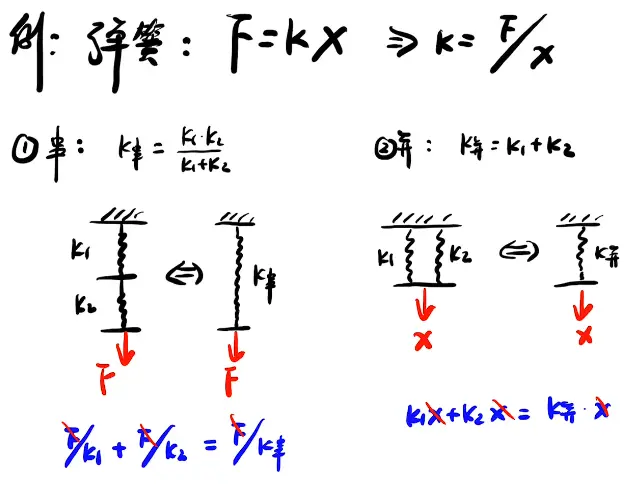
弹簧的串并联
4. 力矩

r为位矢,其选择与坐标系有关
第二课时
1. 平衡
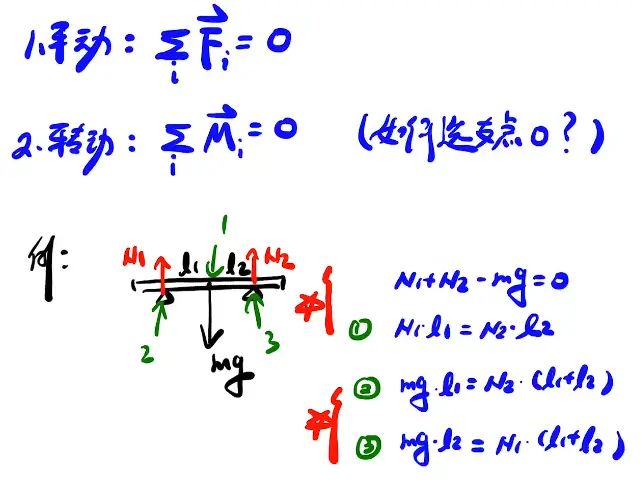
以不同参考系列出的平衡⚖方程不同。
以下为数学证明。
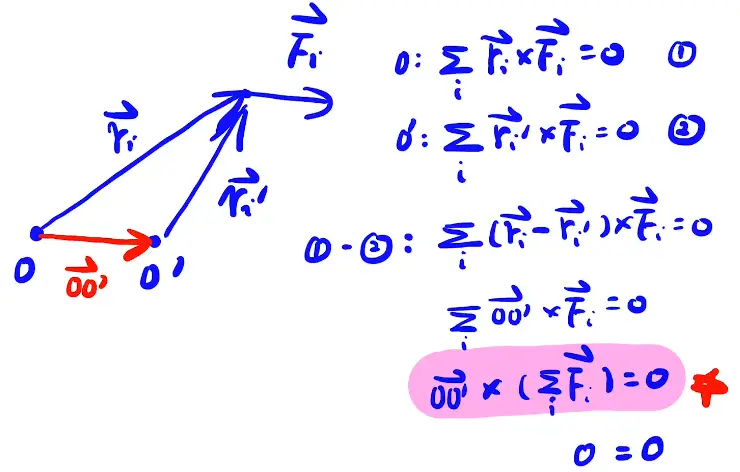
ps:如果列了合外力等于0,不要换参考点。另外列两个合外力矩等于0只能证明 F 与 OO' 平行
2. 力偶
3. 全反力
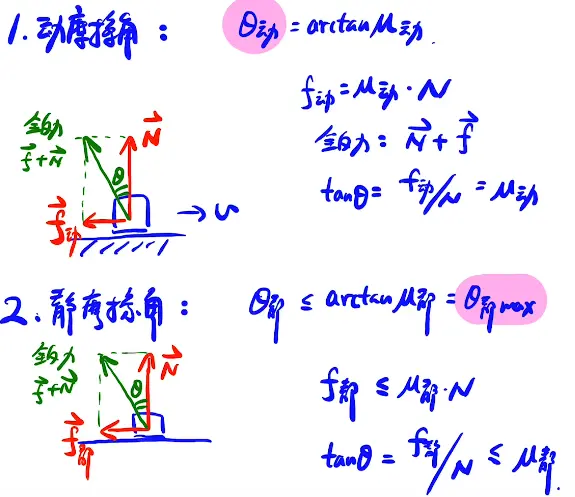
4. 有质量绳
- 一段竖直放置的长度为L的绳子,在x处(从上到下)收到的张力为$\dfrac{L-x}{L}G$
- 若为一段曲线
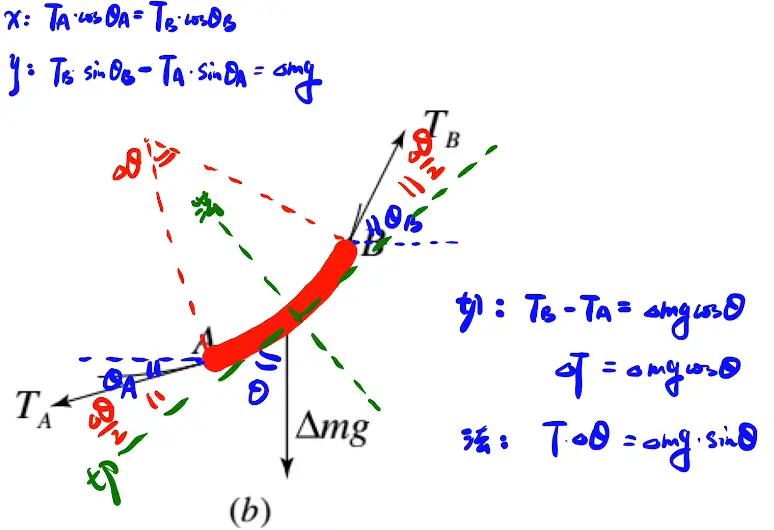
对于法向的解释:两个T的合力$T\sin \dfrac{\theta }{2}\cdot 2=T\theta$
5. 平衡
- 能量的导数是负的合外力,平衡时也对应E的极值
- 分类(摘自百度百科)
- 不稳定平衡:处于平衡状态的物体,由于受到某种外界微小的作用,如果物体稍有偏离就不能恢复到原来的平衡状态,这种情况叫“不稳定平衡”。例如,当一个圆球体放在一个凸起的圆盘上,或是一个圆锥体,以其尖端竖立在一个平面上,这些物体都处于不稳定平衡状态。翻倒后,一直要等到它们的重心相对地取得最低位置时,这些物体才会静止不动。即任何微小的运动都能使其重心降低的物体,一定处于不稳定平衡状态之下。
- 稳定平衡:凡能在被移动离开它的平衡位置后,仍试图回复其原来位置(此时其重心比较低)从而恢复到原来的平衡状态的物体,它原来的平衡状态叫“稳定平衡”。例如,圆球体在一个凹进的圆盘中时;一圆锥体以其底面竖立时,都属于稳定平衡状态。
随遇平衡:物体在外界作用下,它的平衡状态不随时间和坐标的变化而改变。这些物体如被移置到一个新的位置时,虽然它们不能自动地恢复其原来的位置,但它们在新的位置上,却仍能停住不动,其重心之高度,亦保持不变。一般说来,任何微小之运动,既不能将其重心提高,亦不能使其重心降低之物体,一定处于随遇平衡状态之下。
例题

[x-card title='解法' fold='on']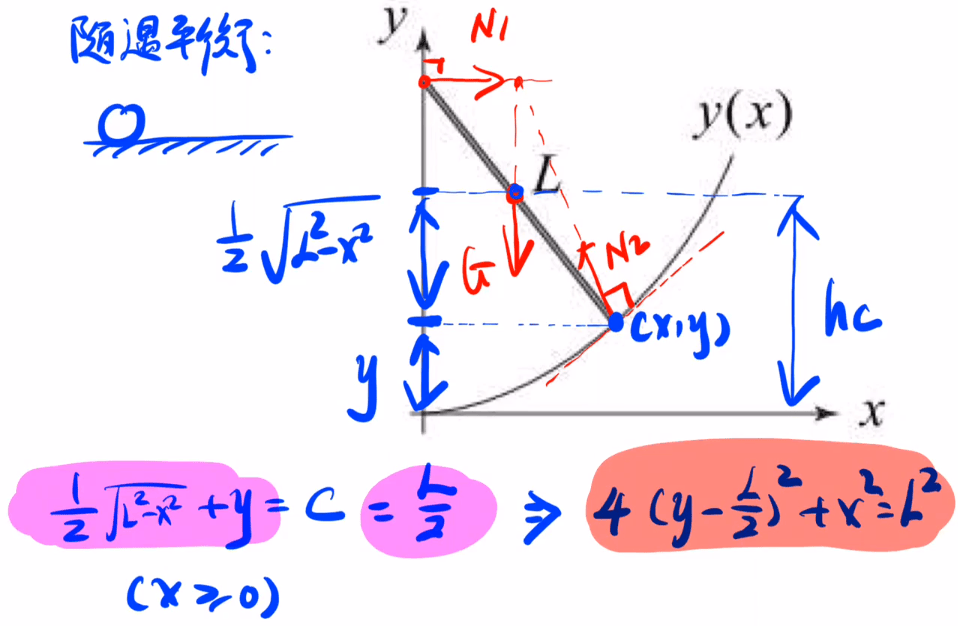
随遇平衡就是重心不变
[/x-card]
- 有点用的总结:微扰后看重心位置。物体的重心位置越低,物体的稳定程度越高。若是升了则稳定,若是降了则不稳定。若不升不降则为随遇。
数学中的奇技淫巧
洛必达法则
导数取到极值时导数值为0,这样可推出两个原函数与两个导数比值相等。即,由此可以快速求出极值。
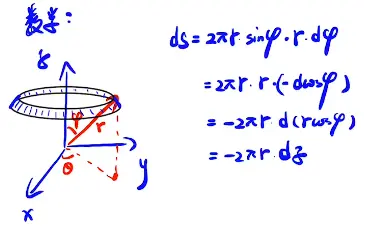
求圆的表面积公式
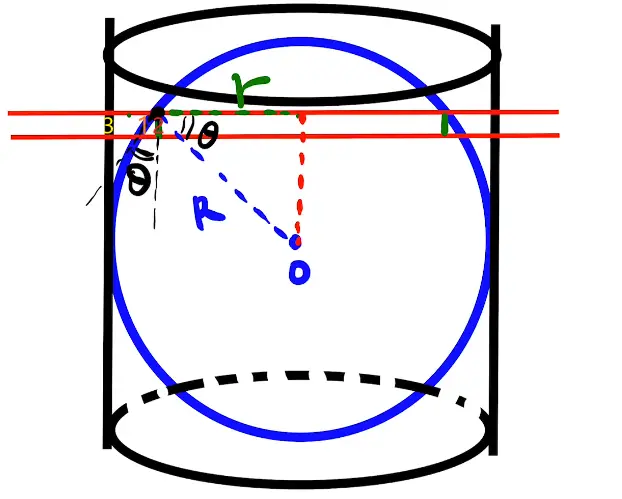
方法一:
如图所示两个θ角相等,2与1的面积比为cosθ,又因为$\cos \theta =\dfrac{r}{R}$,所以1与3面积相同,可得圆与圆柱表面积相等
方法二:
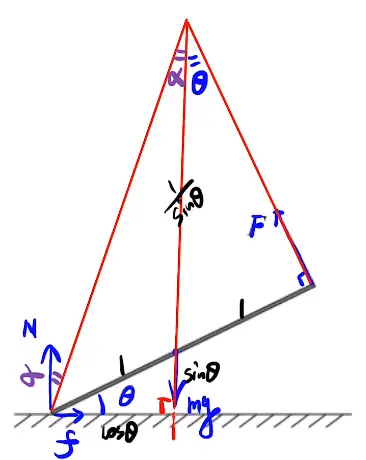
三角函数计算
通过设1来表示边, 例如
巴普斯定理
1、在一平面上取任一闭合区域,其面积为S,使它沿垂直于该区域的平面运动形成一个体积为V的立体,那么这个立体图形的体积就等于质心所经路程 r 乘以区域面积。表达式为V=S·r。
2、如果令某一长为L的曲线段,其长度为L,使它沿着垂直于它所在平面的方向扫过一个面积S,那么这个面积的大小就等于线段质心移动的距离r乘以线段的长度。表达式为S=L·r。