静力学

第一课时-物理概念

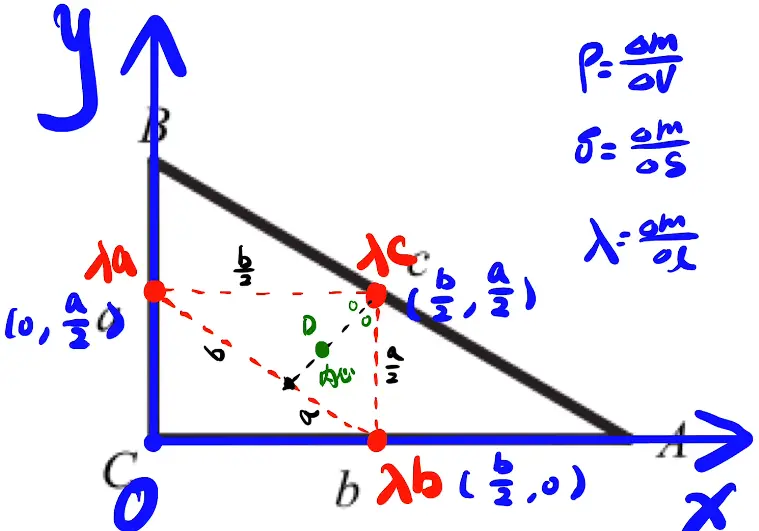
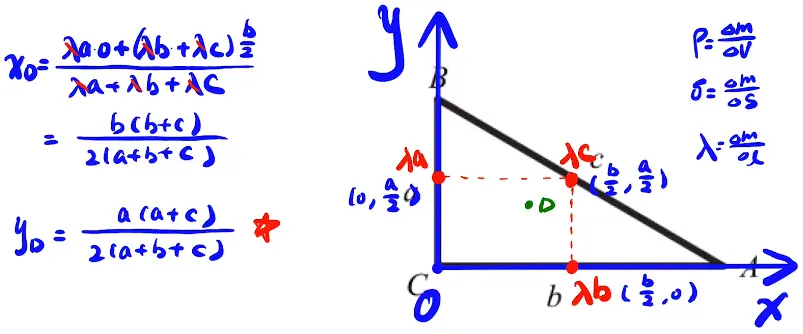
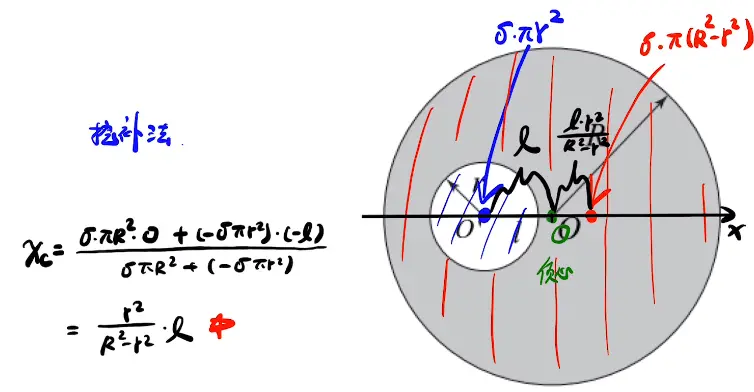
1. 重心

[x-card title='数学解法' fold='on']

[/x-card][x-card title='几何解法' fold='on']

运用了角平分线定理（如果三角形一边上的某个点与这条边所成的两条线段与这条边的对角的两边对应成比例，那么该点与对角顶点的连线是三角形的一条角平分线。）

[/x-card]

[x-card title='解法' fold='on']

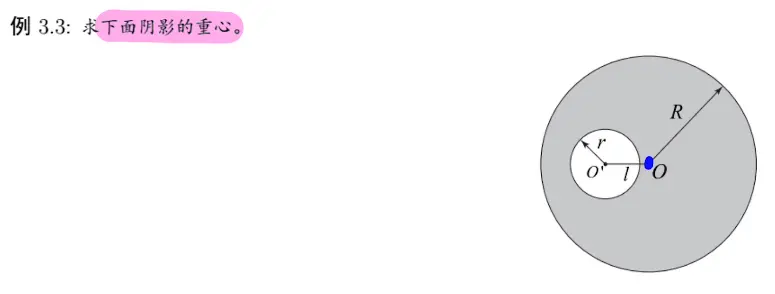
[/x-card]

2. 妙妙妙

[x-card title='解法' fold='on']
边际量，当水面不到重心时，中心会下降，而当水面到达中心之后，重心会上升。所以水面在重心上时有最小值
[/x-card]

3. 弹力

• 一个质量为m，劲度系数为k的弹簧竖直放置，则自身的压缩量为多少

  [x-card title='解法' fold='on']小量分析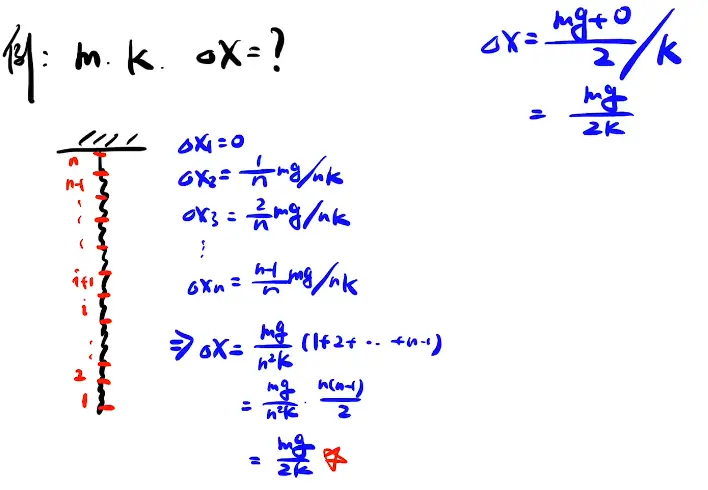
  
  [/x-card]

4.力矩应用

[x-card title='解法' fold='on']
1.（分开做）四力两两合成后，右边合力水平向左，再用矢量三角形得最小值$\dfrac{1}{2}mg$
2. （整体法）
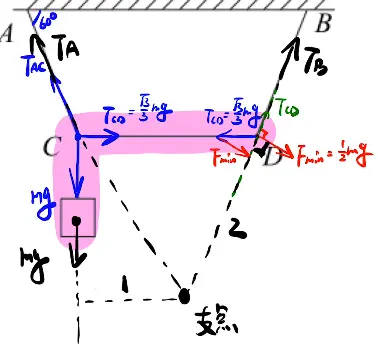
找参考点，去除两个T，F最小时垂直于力矩
[/x-card]

第二课时-平衡问题

1. 三个球

[x-card title='解法' fold='on']

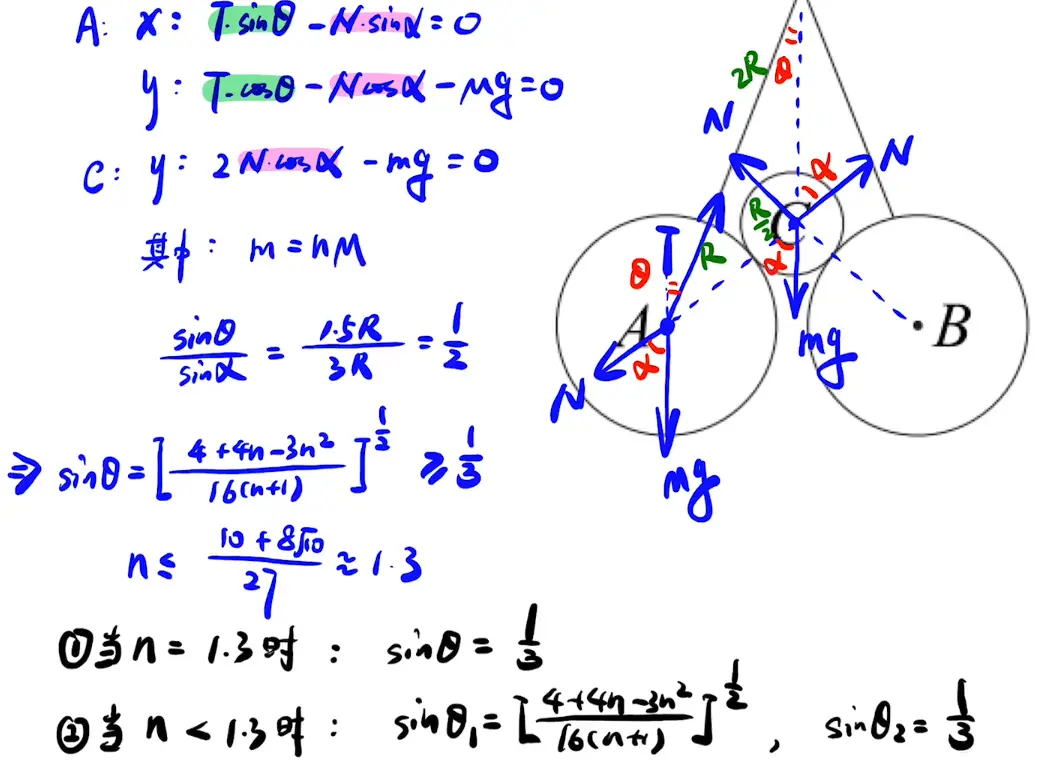
第二种的1/3这种情况是AB原本碰在一起，加上轻小球后夹角不会改变。
得出解后要考虑实际意义[/x-card]

2. 力矩

[x-card title='解法' fold='on']

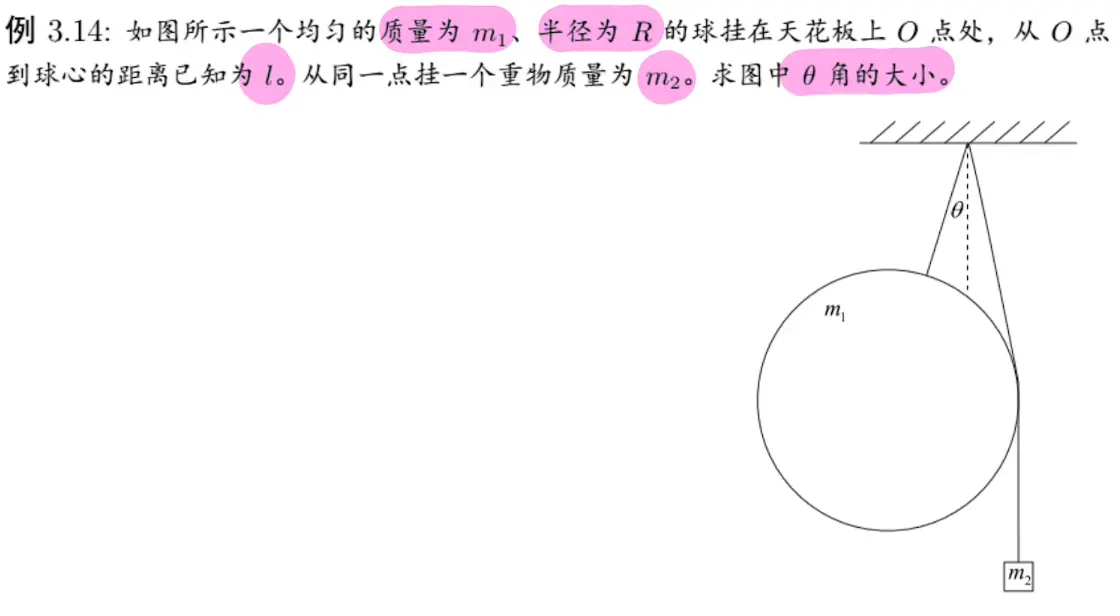
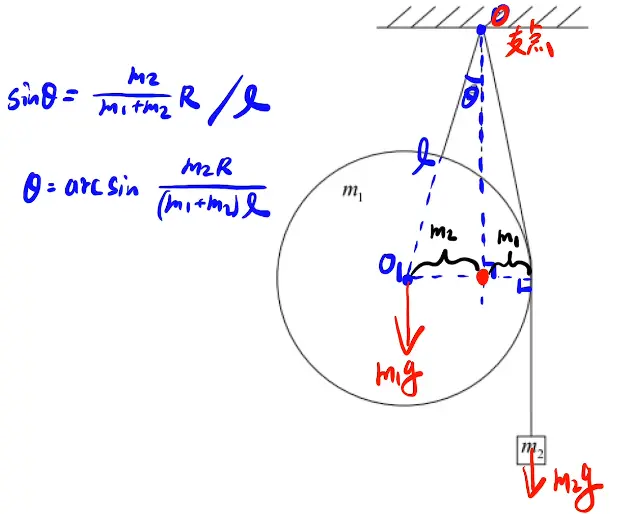
力矩的计算选定旋转轴之后可寻找便利的支点进行计算
[/x-card]

[x-card title='解法' fold='on']
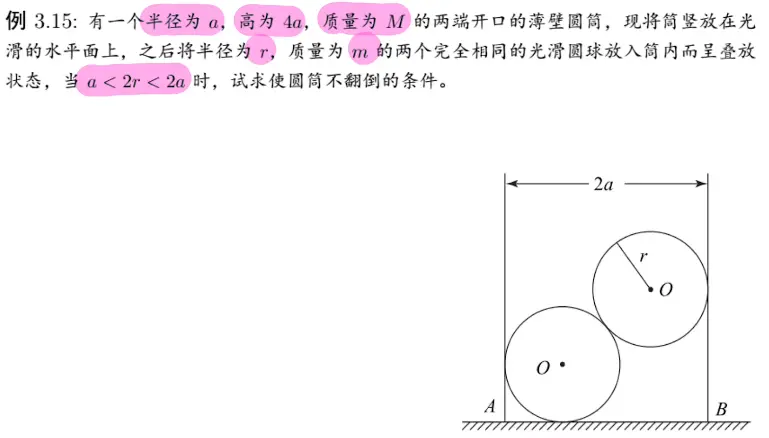
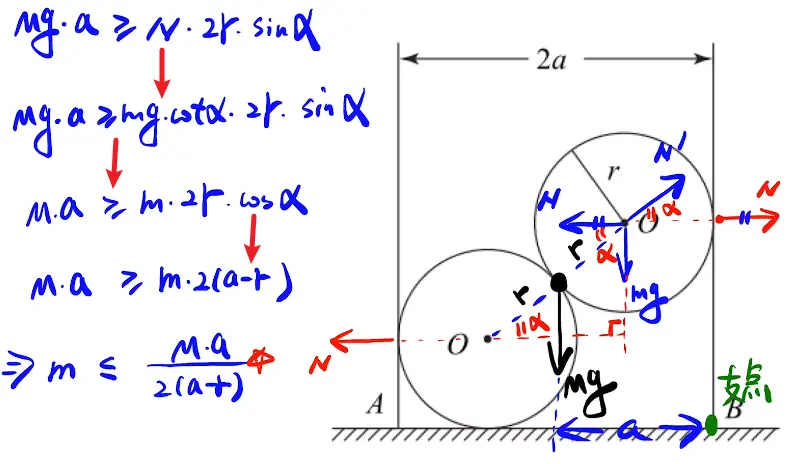
一个式子进行化简与求解，不要过早进行化简

[/x-card]

3. 整体法

[x-card title='解法' fold='on']

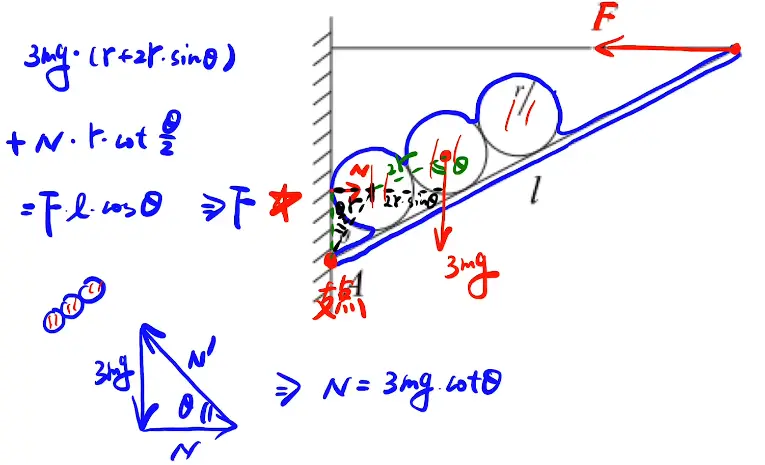
首先以三个球+杆为整体，再以三个球为整体
[/x-card]

4. 全反力

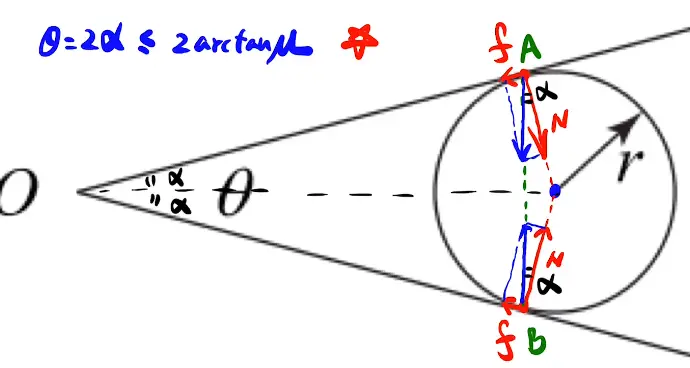
[x-card title='解法' fold='on']

[/x-card]

[x-card title='解法1' fold='on']
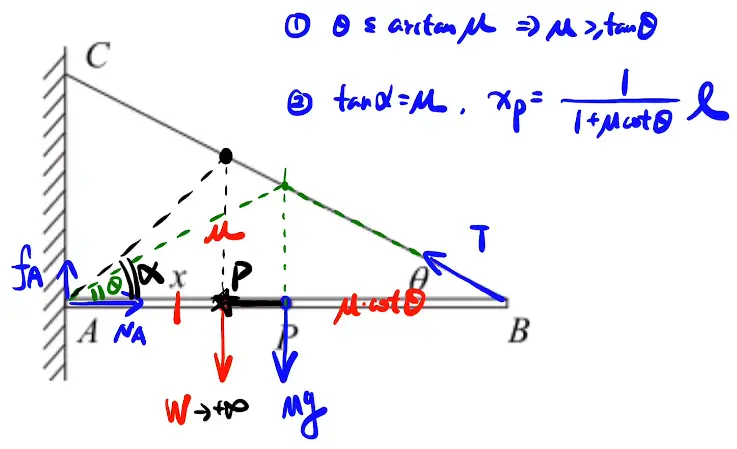
第二问中让W趋于无穷大即可的M本身即为两个重力的等效点

[/x-card][x-card title='解法2' fold='on']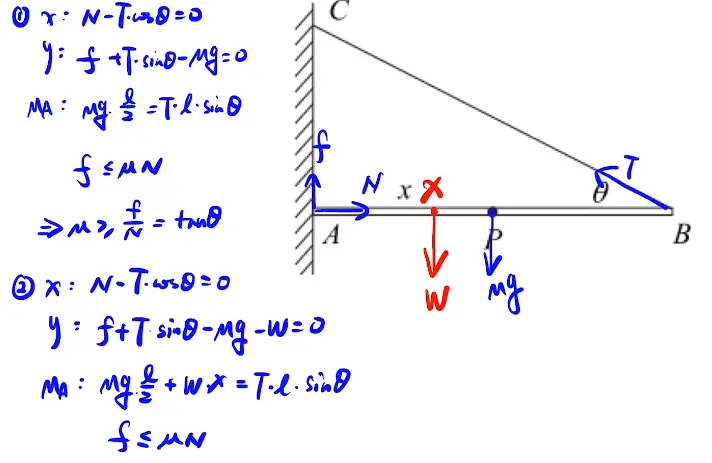

[/x-card]

[x-card title='解法' fold='on']

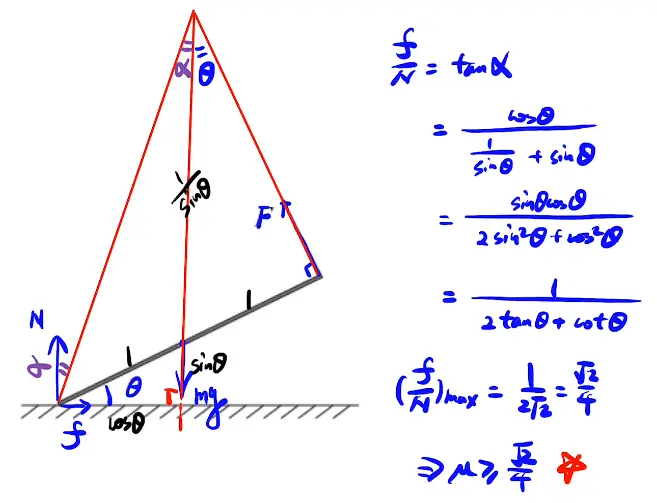
[/x-card]

5.三维空间的受力分析

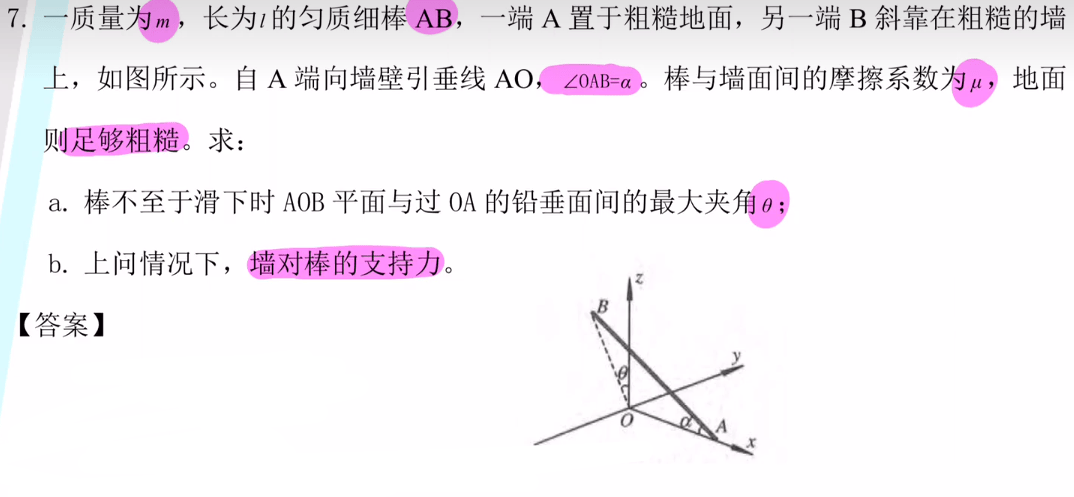
[x-card title='解法' fold='on']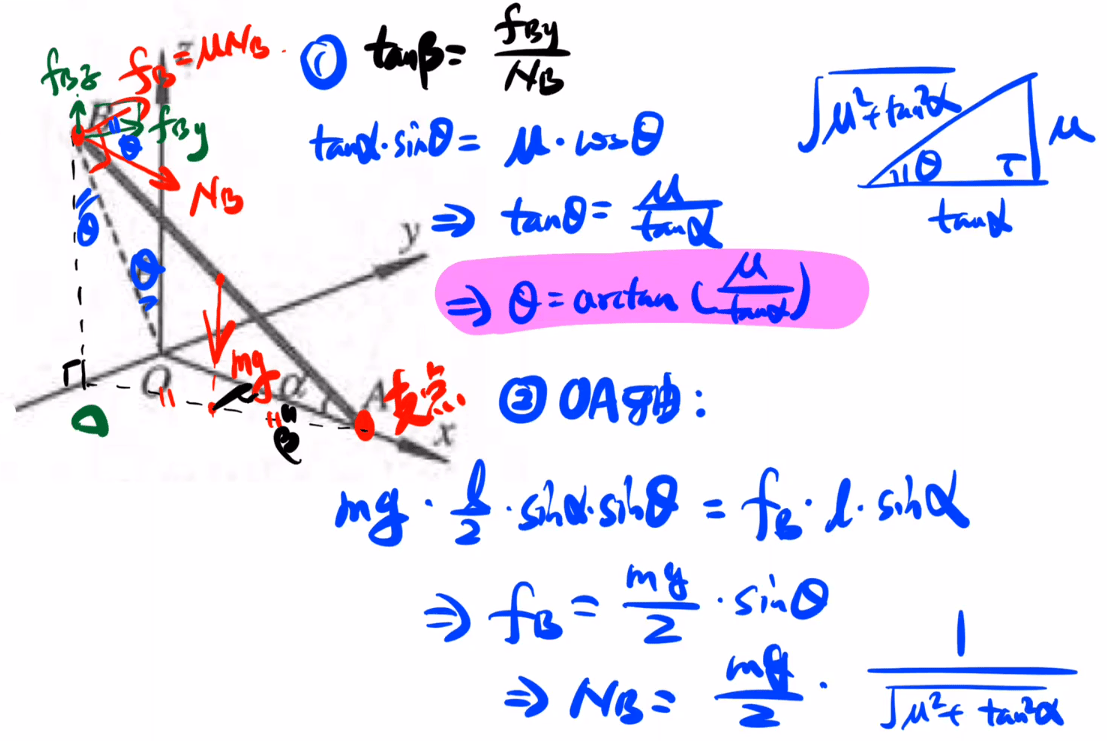
1.将三维受力先简化成二维问题：在同一个平面上
2.选择力矩进行研究时可以通过确定旋转轴大大减小计算量
[/x-card]

第三课时-张力问题

1. 有质量绳

[x-card title='解法' fold='on']

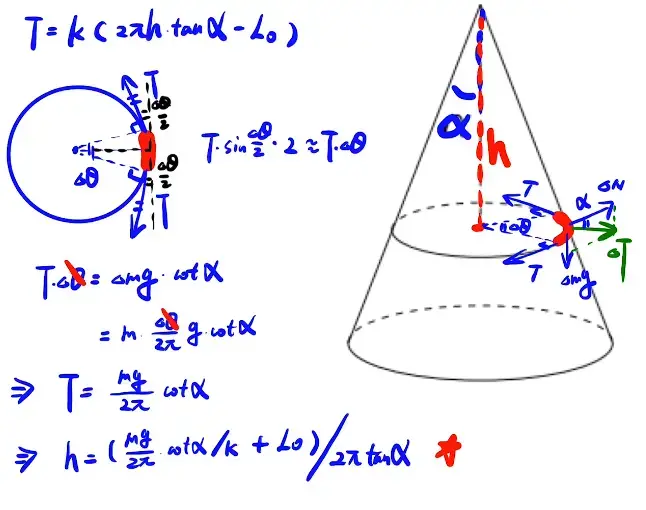
整体法与隔离法的应用，第一个式子为看整个绳子，第二个看一小段。
[/x-card]

[x-card title='解法' fold='on']

[/x-card]

2. 半圆绳

[x-card title='解法' fold='on']
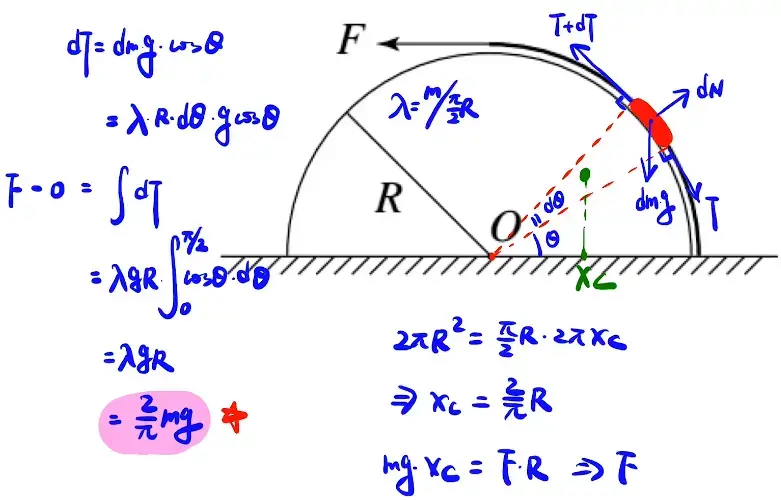
1.利用微积分进行分析
2.利用巴普斯定理求出质心位置，之后利用力矩平衡计算
3.记住结论

[/x-card]

3. 绳子下垂

[x-card title='解法' fold='on']

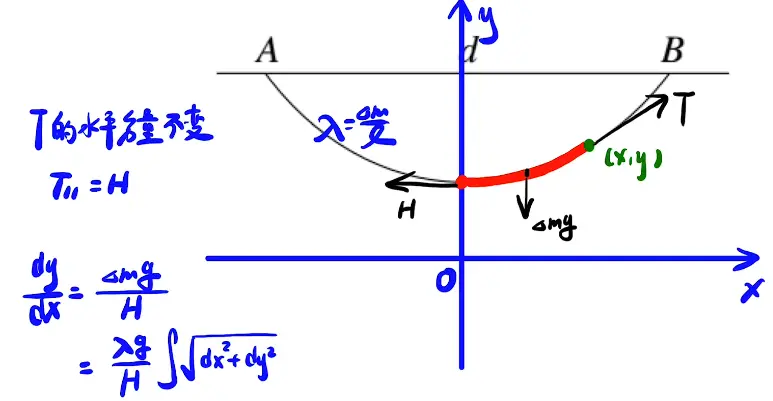
[/x-card]

第四课时-三类平衡

1. 弹簧

[x-card title='解法' fold='on']
1.使其有微小的位移
2.以重力力矩大于弹力力矩列式子求解

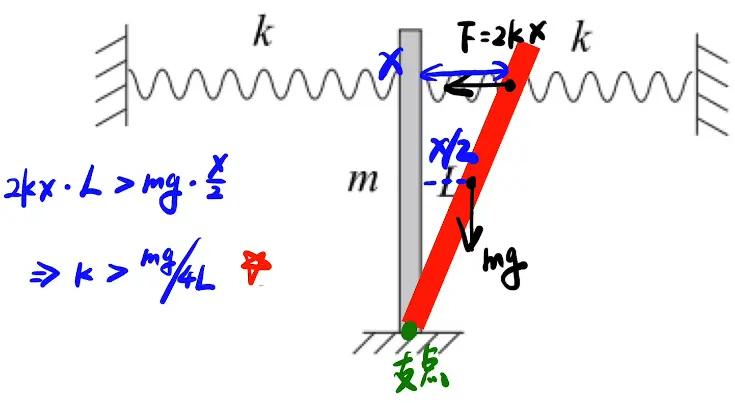
[/x-card]

2. 另解

[x-card title='解法' fold='on']

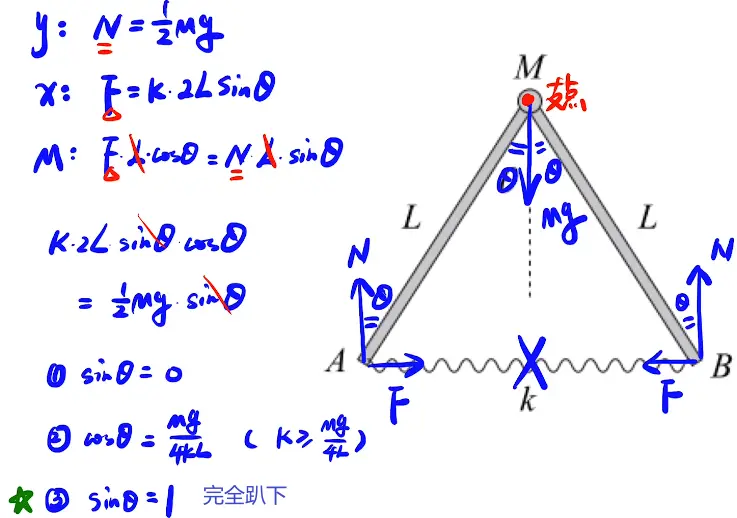
[/x-card]

3. 随遇平衡

[x-card title='解法' fold='on']
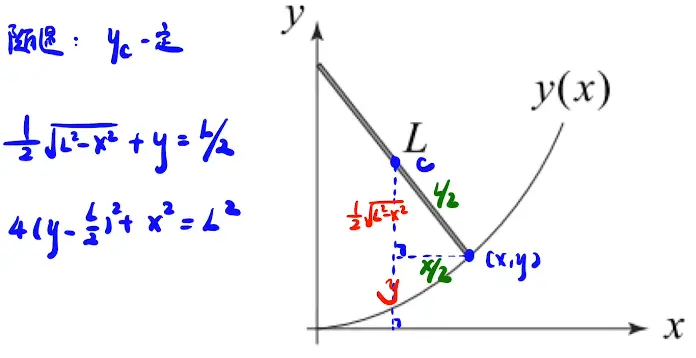
[/x-card]

4. 碗和球

[x-card title='解法' fold='on']
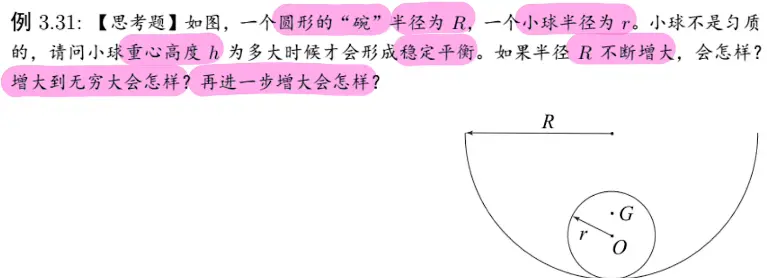
充分利用各种几何关系进行求解

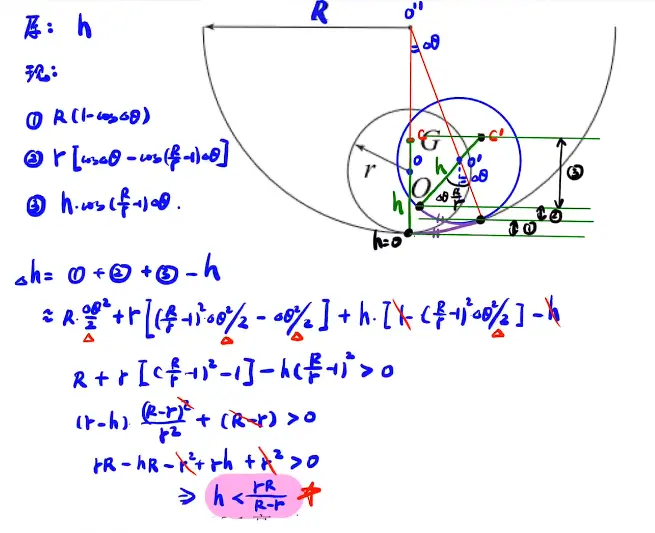
[/x-card]