运动学习题
第一课时-一维运动
1. 微积分·壹
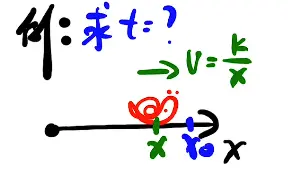
\int_{0}^{t}dt=\dfrac{1}{k}\int^{x}_{x_{0}}xdx\ t=\dfrac{1}{2k}\times \left(
x^{2}-x_{0}^{2}\right) \end{aligned}$[/x-card]
2. 相对运动

 [/x-card]
[/x-card]3. 自相似
- 一

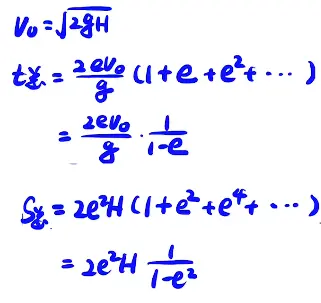
(注意其中公式 $ v^{2}=2ax $的运用)[/x-card]
- 二

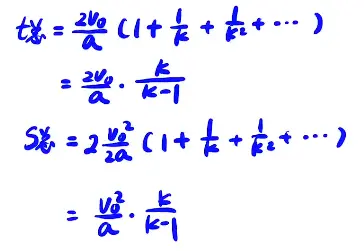
[/x-card]
4. 周期


ps: 若记相邻黑点所示时间为t,则T要满足相隔1,3,5,7,··· (2n-1)个t,且上半部分与下半部分时间需要相等[/x-card]
第二课时-速度及加速度
1. 类比与变分

[x-card title='解法一(变分)' fold='on']首先补充一个思想,
“变分”
变分法是处理泛函的数学领域,和处理函数的普通相对。譬如,这样的泛函可以通过未知函数的积分和它的导数来构造。变分法最终寻求的是极值函数:它们使得泛函取得极大或极小值。有些曲线上的经典问题采用这种形式表达:一个例子是最速降线,在重力作用下一个粒子沿着该路径可以在最短时间从点A到达不直接在它底下的一点B。在所有从A到B的曲线中必须极小化代表下降时间的表达式。
——来自维基百科
变分,按这位老师所说就是取极限时两边具有等时性(感觉挺玄学的,以后再看看吧),先看图。
ps:类比成一道光。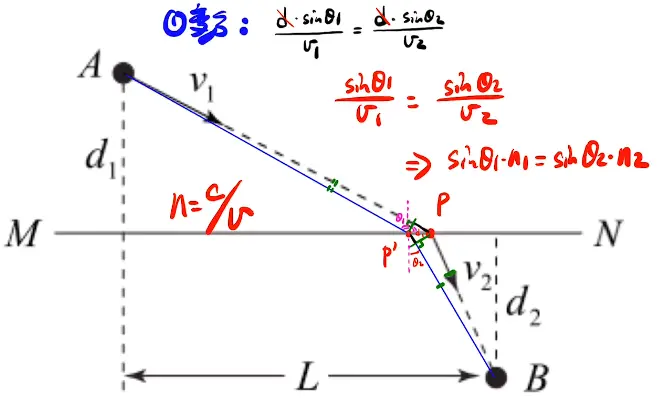 [/x-card]
[/x-card]
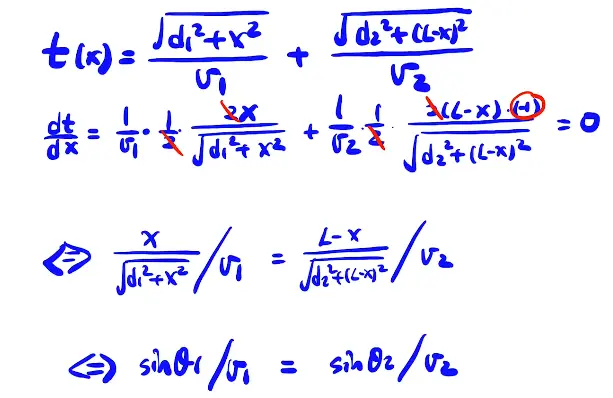 [/x-card]
[/x-card]2. 加速度分解
30UG2P]LWG]QW}HI5.webp)
因为匀速我们知道斜面对物体的作用力是竖直向上的
所以当斜面加速下落的时候
斜面对物体的力仍然是竖直向上的
物体在水平方向上合力为零 所以是个匀速运动
因此既然不脱离斜面 它在竖直方向上也是匀速运动(相对于电梯)[/x-card]
3. 抛体

 [/x-card]
[/x-card]
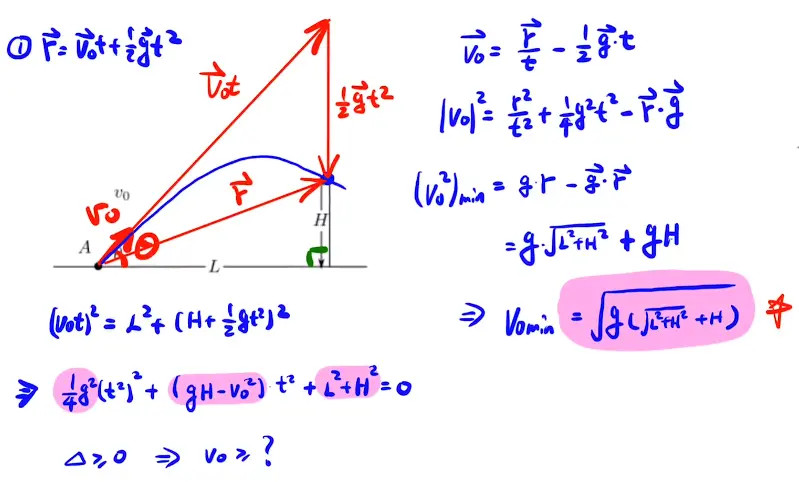 [/x-card]
[/x-card]
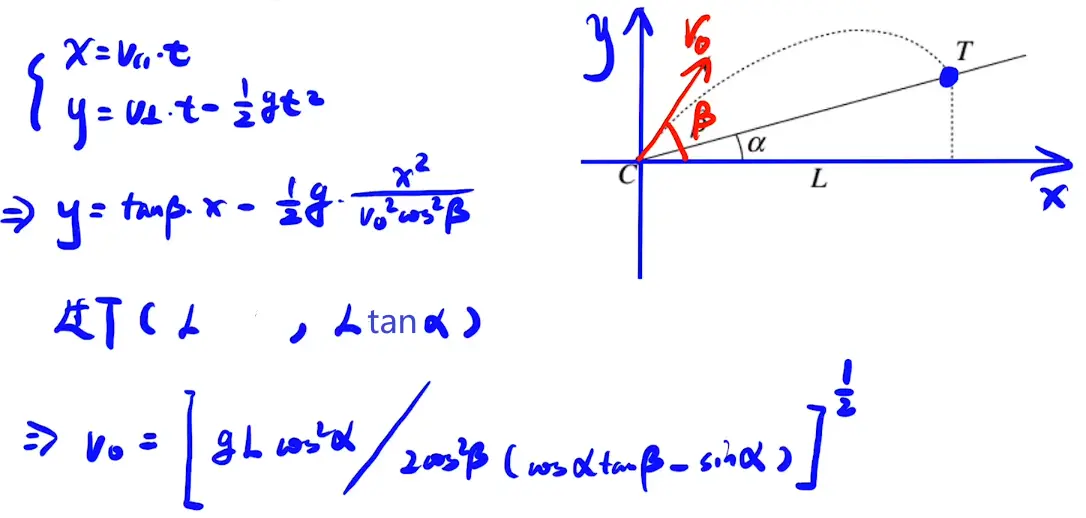 [/x-card]
[/x-card]
=\dfrac{2H}{L}$答案[/x-card]
4. 抛体+周期
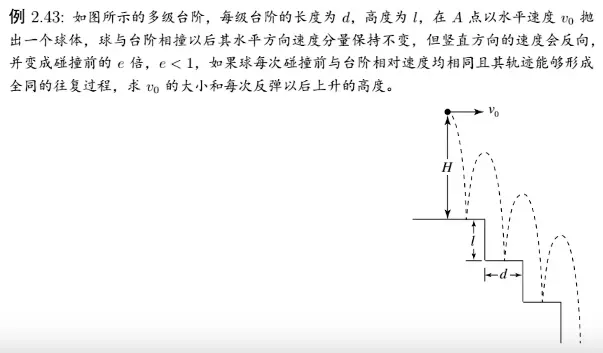
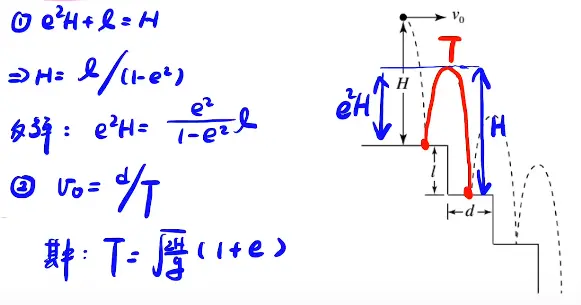 [/x-card]
[/x-card]
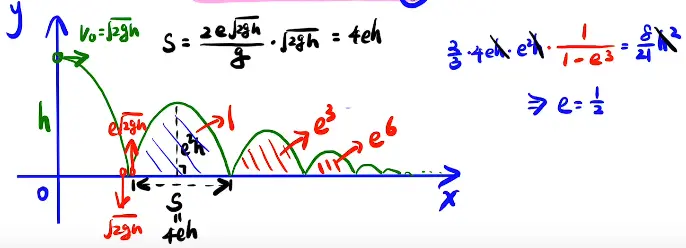 [/x-card]
[/x-card]
1. 能量观的加强,从地面到P速度大小插值是一定的!!
2. 从逆方向来考虑,从P点跳下去,反做
3. 包络线与圆相切是v的最小值
4. 强大的计算能力!!!!(增根)
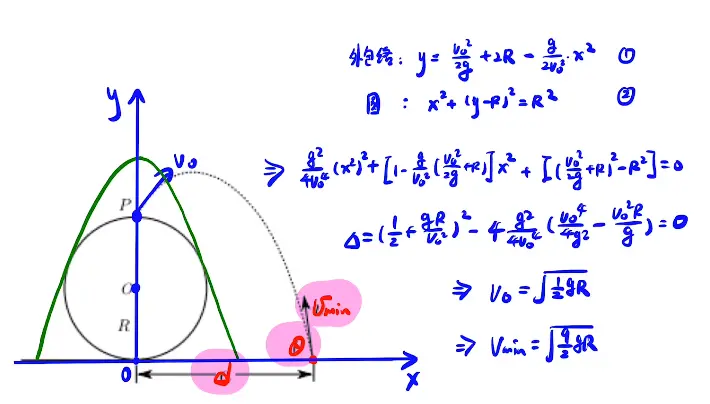
[/x-card]
第三课时-圆周运动
1. 相对角速度
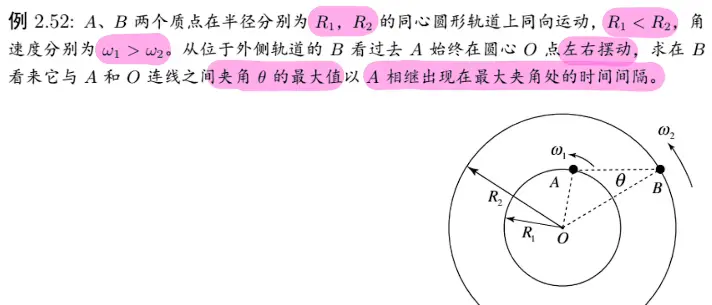
[x-card title='解法' fold='on'] [/x-card]
[/x-card]
2. 微积分·贰
- 微积分的使用

 [/x-card]
[/x-card]3. 摆线
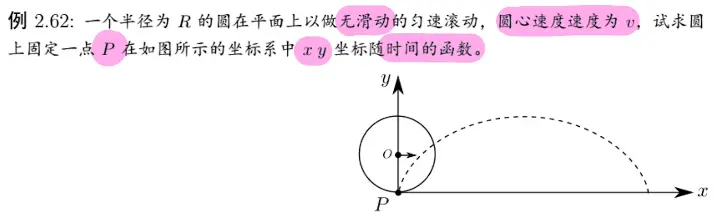
 [/x-card]
[/x-card]第四课时-综合运用
1. 微积分·叁

 [/x-card]
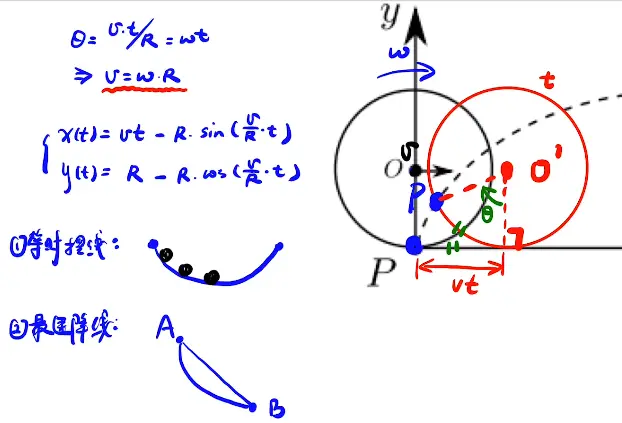
[/x-card]2. 相对运动

 [/x-card]
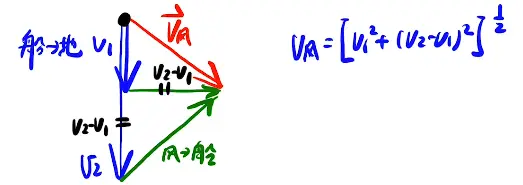
[/x-card]3. 相对运动压轴

 [/x-card]
[/x-card]4. 经典狗追兔子

- 根据已知信息画图理解题意
2. 列出方程
3. 相对位移中的H与y方向分解的H意义不完全一样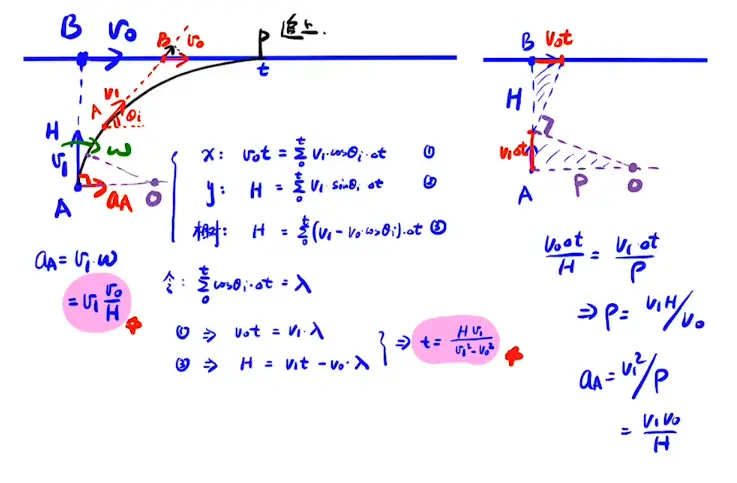 [/x-card]
[/x-card]
变式:
若速度均为v则不能追上,则相距最近应该是多少
[x-card title='解法' fold='on']暂无[/x-card]
第五课时-约束运动
1. 杆与墙面
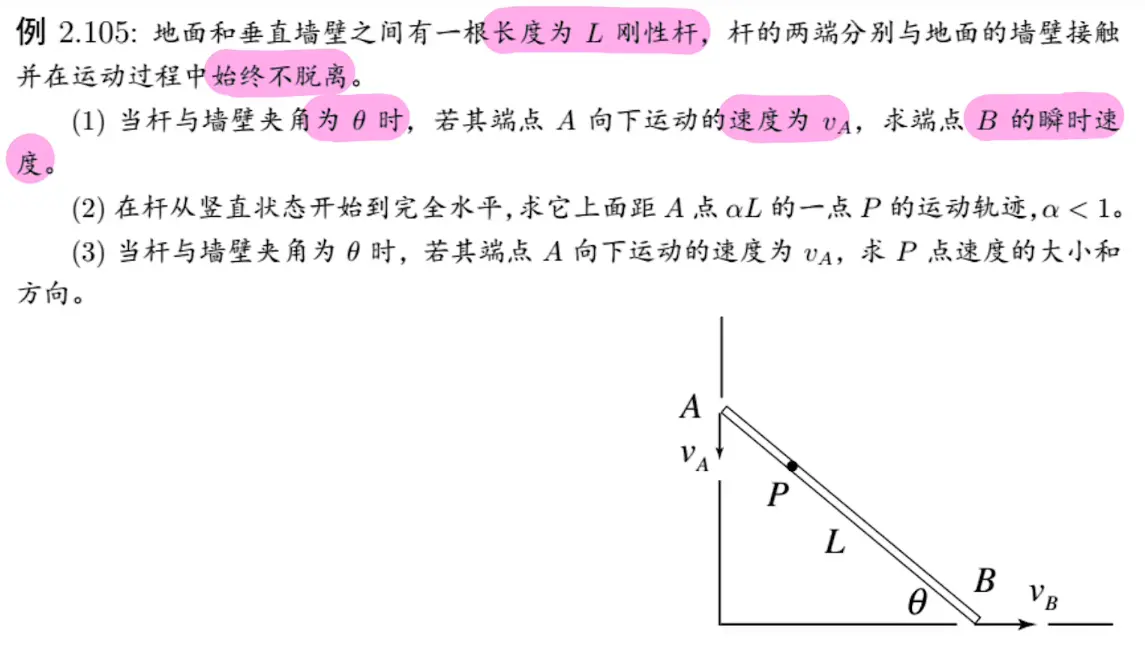
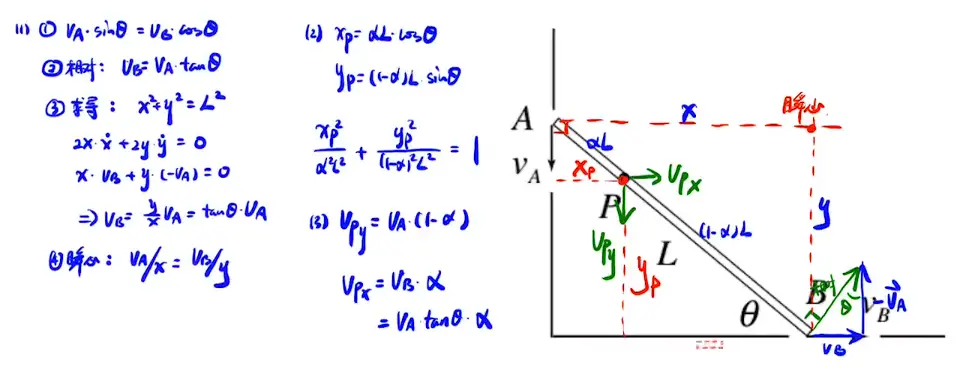 [/x-card]
[/x-card]2. 点与面

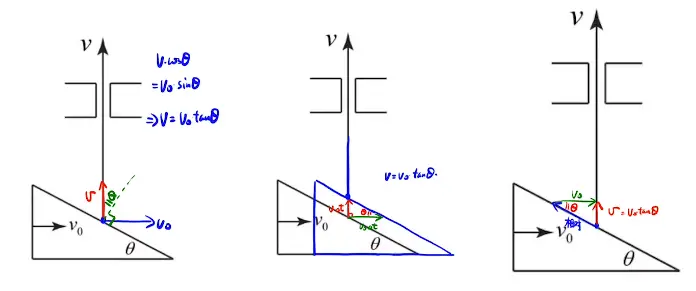 分别运用的原理为
分别运用的原理为1. 法向速度为0
- 转到位移来求,画图
- 运用相对运动 [/x-card]
3.相对运动

[x-card title='解法' fold='on']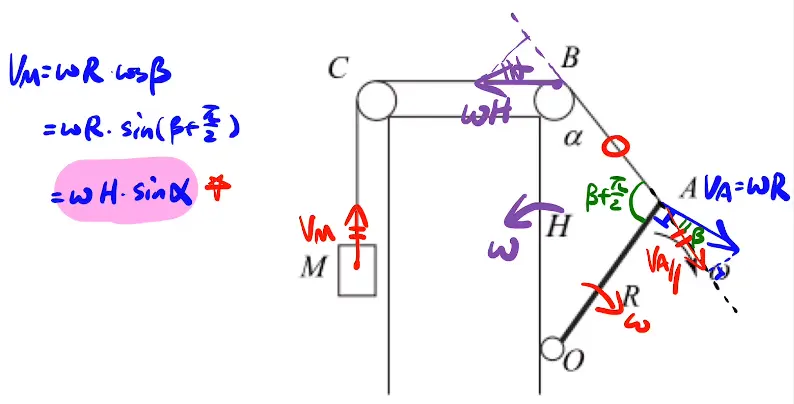
第一种方法注意找角的关系
第二种方法如紫色图,H相对R以ω的角速度运动
[/x-card]
第六课时-刚体运动
1. 滚动
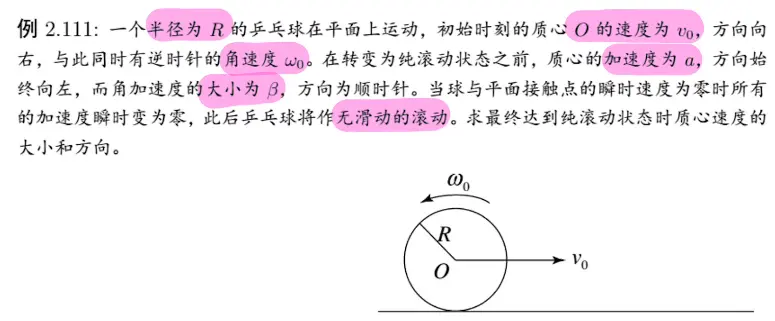

[/x-card]






















































































































































test